Целочисленное линейное программирование
Пример Найти решение задачи линейного программирования f= 2 x 1+ x 2→ min,
Приведем задачу к каноническому виду в части ограничений. Для этого вычтем из левой части неравенств фиктивные переменные х 3 и х 4.
Полученные в результате преобразования ограничения имеют непредпочтительный вид. Воспользуемся М-методом. Прибавим к левым частям уравнений ограничений переменные ω 1 и ω 2.
Целевая функция примет вид: F=M (ω 1+ ω 2)→min. Приведем целевую функцию к каноническому виду: F ' = – M (ω 1+ ω 2)→mах, то есть F ' = – Mω 1 – M ω 2→mах. Таким образом, приведенная к каноническому виду задача имеет следующий вид F ' = – Mω 1 – M ω 2→mах,
Решим полученную задачу симплекс-методом. Составим симплекс-таблицу. Таблица 6.1.
Начальное решение Х 0={ х 1=0, х 2=0, х 3=0, х 4=0, ω 1=6, ω 2=12} не является оптимальным, так как среди оценок в d -строке есть отрицательные, значит решение Х 0 можно улучшить. Определим переменную, которая войдет в список базисных. Для этого найдем максимальную по абсолютному значению d -оценку среди отрицательных. max{|-2 M |, |-4 M |}= 4 M. Значит, разрешающим будет второй столбец, а в базис войдет переменная х 2. Таблица 6.2.
Теперь определим переменную, которая выйдет из базиса, для чего вычислим отношения элементов столбца свободных членов к соответствующим элементам разрешающего столбца и среди полученных отношений найдем минимальное:
Значит разрешающей строкой будет вторая, из базиса выйдет переменная ω 2 и разрешающий элемент а 22=3.
Таблица 6.3.
Перейдем к новой симплекс-таблице. Разрешающий элемент при пересчете должен стать единицей, а остальные элементы в разрешающем столбце стать нулями. Для этого элементы разрешающей строки поделим на разрешающий элемент 3. Таблица 6.4.
Для того чтобы элемент, стоящий в разрешающем столбце в первой строке стал нулем, умножим разрешающую строку на -1 и прибавим ее к первой строке. Таблица 6.5.
Теперь в базисе вместо переменной ω 2 переменная х 2 и d -оценки надо пересчитать. Таблица 6.6.
Полученное решение Х 1={ х 1=0, х 2=4, х 3=0, х 4=0, ω 1=2, ω 2=0} не является оптимальным, так как среди оценок в d -строке есть отрицательные, значит решение Х 1 можно улучшить. Определим переменную, которая войдет в список базисных. Для этого найдем максимальную по абсолютному значению d -оценку среди отрицательных:
Значит, разрешающим будет первый столбец, а в базис войдет переменная х 1.
Таблица 6.7.
Теперь определим переменную, которая выйдет из базиса, для чего вычислим отношения элементов столбца свободных членов к соответствующим элементам разрешающего столбца и среди полученных отношений найдем минимальное:
Значит разрешающей строкой будет первая, из базиса выйдет переменная ω 1 и разрешающий элемент а 11= Таблица 6.8.
Перейдем к новой симплекс-таблице. Разрешающий элемент при пересчете должен стать единицей, а остальные элементы в разрешающем столбце стать нулями. Для этого элементы разрешающей строки поделим на разрешающий элемент Таблица 6.9.
Далее умножим элементы разрешающей строки на - Таблица 6.10.
В списке базисных переменных вместо ω 1 теперь х 1 и d -оценки также изменятся. Таблица 6.11.
Полученное решение Х 2={ х 1=3, х 2=2, х 3=0, х 4=0, ω 1=0, ω 2=0} оптимально, так как среди оценок в d -строке нет отрицательных. Подставим полученные значения переменных в изначальную целевую функцию f: f= 2·3+2=8. Минимальное значение целевой функции f= 8 достигается при х 1=3, х 2=2.
Целочисленное линейное программирование
Математическая модель задачи целочисленного линейного программирования имеет вид:
Здесь Z – множество целых чисел. Задачи целочисленного линейного программирования решаются при помощи различных методов. Рассмотрим два из них: метод Гомори (метод отсечений) и метод ветвей и границ. Метод Гомори (метод отсечений) Данный метод содержит два этапа. 1 этап: решение исходной задачи линейного программирования симплекс-методом и проверка решения на целочисленность. Если решение содержит хотя бы одно дробное значение, то переходят к этапу 2, в противном случае задача решена. 2 этап: составление дополнительного ограничения (сечения) и решение расширенной задачи симплекс-методом. Дополнительное ограничение отсекает нецелочисленные решения задачи. После решения новой расширенной задачи симплекс-методом, переходим к этапу 1 и т.д.
Сечение обладает следующими свойствами: 1) любое целочисленное решение удовлетворяет ему; 2) любое нецелочисленное решение задачи не удовлетворяет ему.
Составление сечения.
Пусть после 1 этапа получено решение: X= { x 1= b 1, x 2= b 2, …, xi = bi, …, xm = bm, xm +1=0, …, xn =0}, где bi – дробное число. Так как в решении задачи присутствует дробное число, значит переходим к этапу 2 и составляем дополнительное ограничение. Новое ограничение (сечение) составляется на основе строки, которой соответствует дробное число bi и будет иметь вид:
Здесь αi j - это дробная часть коэффициентов аij: αi j ={ аij }, j = βi - это дробная часть числа bi: βi ={ bi }. Напомним, что дробная часть является разницей между числом и его целой частью: { а }= а – [ а ]. Например, {2,3}=2,3 – [2,3]=2,3 – 2 =0,3. {-5,6}=-5.6 – [-5,6]=-5,6 – (-6) = 0,4. В примере с отрицательным числом целая часть равна -6, так как целая часть – это ближайшее меньшее целое число, т.е. происходит округление до целого в меньшую сторону. Для того, чтобы привести вновь составленную систему ограничений к каноническому виду, требуется преобразовать неравенство в равенство. Введем фиктивную переменную xn +1. αi m +1 x m +1 + αi m +2 x m +2 +…+ αi n x n – xn +1= βi, xn +1≥0.
Замечание: Если в результате решения задачи получилось несколько дробных чисел в ответе, то требуется выбрать одно из них. Для составления отсечения выбирается число, у которого максимальна дробная часть.
Пример Решить задачу: f= 3 x 1+2 x 2→max
После выполнения этапа 1 при решении задачи симплекс-методов получилась следующая таблица.
 , х 2= , х 2=  , f = , f =  . Как видно, в ответе присутствуют два дробных числа: . Как видно, в ответе присутствуют два дробных числа:  и и  . Применим метод Гомори для получения целочисленного решения. . Применим метод Гомори для получения целочисленного решения.
Во-первых, выберем число с максимальной дробной частью: { Это означает, что сечение будет составлено на основе строки, соответствующей числу Во-вторых, составим ограничение. Для этого выпишем линейную комбинацию чисел из строки, соответствующей числу 0 х 1+1 х 1 Воспользуемся формулой (7.3) и получим:
Упростим полученное отсечение, сократив на множитель: х 3+ х 4≥1. Приведем новое ограничение к каноническому виду: – х 3– х 4 ≤– 1, – х 3– х 4+ х 5 =– 1, х 5≥0. Добавим новое сечение к системе ограничений задачи: f= 3 x 1+2 x 2→max
Решив новую задачу симплекс-методом, получим целочисленное решение: х 1=3; х 2=2; f =13.
Метод «ветвей и границ» Метод «ветвей и границ» - это метод направленного перебора множества вариантов решений задачи. Алгоритм метода «ветвей и границ» 1. Строятся вершины первого уровня. Для каждой вершины подсчитывается оценка нижней (верхней) границы. Ветвится вершина, которой соответствует лучшая (минимальная или максимальная) оценка. 2. Для всех вершин i -го уровня (i ≥2) подсчитывается оценка. Ветвится та из висячих вершин уровня i, i –1, i –2, …, 1, которой соответствует лучшая (минимальная или максимальная) оценка. 3. Действие п.2 повторяется до тех пор, пока не будет получено точное решение на последнем уровне, дающее значение целевой функции f*.
Рассмотрим задачу целочисленного линейного программирования (7.1) – (7.2). Пусть в результате решения задачи получили ответ X= { x 1= b 1, x 2= b 2, …, xi = bi, …, xm = bm, xm +1=0, …, xn =0}, где bi – дробное число. Введем два дополнительных условия: xi ≤ zi и xi ≥ zi +1, где [ xi ]= zi.
Два последних неравенства разбивают область допустимых решений для переменной xi на две подобласти. При этом из рассмотрения исключается та подобласть, в которой не содержатся целочисленные значения координаты xi.
Рисунок 7.1. Схематическое изображение решения метода «ветвей и границ».
Пример Рассмотрим задачу из предыдущего примера, решенную методом Гомори. f= 3 x 1+2 x 2→max
В результате решения получился следующий ответ: х 1= х 2 ≤ 1 и х 2 ≥ 2. На основе ветвления получим две новые задачи:
Рисунок 7.2. Ветвление задачи. Таким образом, с помощью двух различных методов получили одно решение задачи целочисленного программирования.
|




 .
.



 .
.
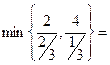 min{3, 12}=3.
min{3, 12}=3. (7.1)
(7.1) (7.2)
(7.2) . (7.3)
. (7.3) ;
;







 и {
и {  }, max{
}, max{  }=
}=  .
.


 Тогда
Тогда





