УСЛОВИЯ НЕПРЕРЫВНОСТИ МОНОТОННОЙ ФУНКЦИИУСЛОВИЯ НЕПРЕРЫВНОСТИ МОНОТОННОЙ ФУНКЦИИ Теорема 1 (об односторонних пределах монотонной функции). Если функция f(x) монотонна и определена в некоторой окрествности U(x0,δ) точки x0, то 1о. 2о. ► Доказательство проведём для неубывающей функции. Т. к. f(x) — неубывающая (по условию Т.) в U(x0,δ), то a* ≤ f(x0) (1) По свойству верхней грани "ε>0 $ x 1Î U(x0,δ) и x 1< x0, такой, что a* – ε< f(x 1 ) ≤ a* <a* + ε. Т.к. f(x) — неубывающая(по условию), то последнее неравенство выполняется " x, удовлетворяющих неравенству x 0 > x > x 1. Т.обр., показали, что "ε>0 $ δ1= x 1– x0 >0 | " x Î U(x0,δ1) Ç D (f) (а значит –δ1< x – x0 <0, что выполняется неравенство a* – ε< f(x) <a* + ε Þ | f(x) – a* | < ε, а значит
(с учетом неравенства (1)). Аналагично даказывается, что
где а* = sup{ x| x≥ x0, Доказать самостоятельно для невозрастающей функции.◄ Следствие из Т.1. Если монотонная функция f (х) имеет разрыв в точке x0, то x0 — точка разрыва перого рода. Теорема 2 (неабходимое и дастаточное условие непрерывности монотонной функции). Для того, чтобы монотонная функция f(x), определенная на промежутке ХÌD(f) была непрерывной, неабходимо и дастаточно, чтобы множество её значений на этом промежутке множество Y={f(x)| xÎX} также являлось промежутком. Необходимость. Дано: f(x) –монотонная, непрерывная функцияна промежутке Х. Доказать: Y – промежуток. ► Доказательство проведём для неубывающей функции. Обозначим через m =inf Y, M =sup Y. Ранее мы договорились считать m = – ¥, если Y – неограниченное снизу множество и M = + ¥, если Y – неограниченное сверху множество. Возьмём любое число l, удовлетворяющего неравенству m < l < M. По 2 свойству верхней (нижней) грани $ x 1, x 2Î Х, (причём x 1 < x2 т.к. по условию f(x) –неубывающая), такие, что m ≤ f(x 1 ) <l< f(x 2 ) ≤ M. По условию теоремы f(x) – непрерывная функцияна промежутке Х, а значит и на отрезке [ x 1, x 2]Ì X Þ по теореме §, что $ с Î[ x 1, x 2]Ì X, такая что f (c)= l. Т. обр. показали, что для любого числа l, удовлетворяющего неравенству m < l < M $ сÎX, в которой f (c)= l Þ Y – промежуток. ◄ Дастаточность. Дано: f(x) –монотонная функцияна промежутке Х. Y={f(x)| xÎX} — промежуток. Доказать: f(x) —непрерывная функцияна промежутке Х. ► Доказательство проведём для неубывающей функции методом от противного. Пусть функция f(x) имеет разрыв в точке x0 Î Х. На основании следствия из Т.1Þ x0 – точка разрыва первого рода, т. е., что
а " x > x0, x ÎX
Объединим (4) и (5), получим что " x ÎX f(x)≠γ, но γÎ Y Þ Y не является промежутком (противоречие). Доказать самостоятельно для невозрастающей функции.◄
|
, при f(x) — неубывающей;
, при f(x) — невозрастающей.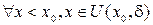
выполняется неравенство f(x)≤ f(x0) Þмножество М= { x| x≤ x0, 
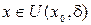} ограничено сверху числом f (x0). По Т. о существ-нии верхней грани $ a* = sup M. По определению верхней грани " х Î U(x0,δ) и x≤ x0 Þ
(2)
, (3)
. Пусть для определённости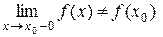 
, тогда по Т.1 
. Рассмотрим число γ, такое, что 
. Тогда " x < x0, x ÎX выполняется неравенство
(4)
(5)
