Зафиксируем любое число  и пакажем, что найдется такое
и пакажем, что найдется такое  , что для всех
, что для всех 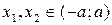 , удовлетворяющих неравенству | x 1– x 2|<
, удовлетворяющих неравенству | x 1– x 2|<  , выполняется неравенство
, выполняется неравенство
| x 12– x 22|<  . Рассмотрим разность
. Рассмотрим разность
(x 12– x 22)=(x 1– x 2)(x 1 + x 2) и заметим, что если  , то модуль суммы
, то модуль суммы
| x 1 + x 2|<2 a. С учетом свойства модуля, получаем неравенство
| x 12– x 22| = | x 1– x 2 || x 1 + x 2|<2 a | x 1– x 2 |. Потребуем, чтобы 2 a | x 1– x 2|<  | x 1– x 2|<
| x 1– x 2|< 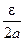 . Тогда для всех
. Тогда для всех  , удовлетворяющих условию | x 1– x 2|<
, удовлетворяющих условию | x 1– x 2|<  , где
, где  =
= 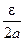 , выполняется неравенство | x 12– x 22|<
, выполняется неравенство | x 12– x 22|<  . Так как
. Так как  – любое положительное число, то функция
– любое положительное число, то функция 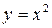 равномерно непрерывная на интервале (– a;a), по определению.
равномерно непрерывная на интервале (– a;a), по определению.
Пример 2. Доказать, что функция  не является равномерно непрерывной на всей числовой прямой.
не является равномерно непрерывной на всей числовой прямой.
► Пакажем, что существует такое число  , что для всех
, что для всех  >0 всегда найдутся
>0 всегда найдутся  , такие, что| x 1– x 2|<
, такие, что| x 1– x 2|<  , але | x 12– x 22|>
, але | x 12– x 22|>  . Возьмем
. Возьмем  =1 и рассмотрим точки
=1 и рассмотрим точки
x 1= 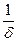 +
+  и x 2 =
и x 2 = 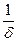 , где
, где  –любое положительное число, они удовлетворяют неравенству
–любое положительное число, они удовлетворяют неравенству
| x 1– x 2|=| 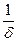 +
+  –
– 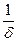 |=
|=  <
< 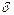 , но | x 12– x 22| = | x 1– x 2|| x 1+ x 2|=
, но | x 12– x 22| = | x 1– x 2|| x 1+ x 2|=  (
(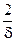 +
+  )=1+
)=1+ 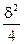 ≥1. Значит
≥1. Значит  не является равномерно непрерывной на всей числовой прямой. ◄
не является равномерно непрерывной на всей числовой прямой. ◄
Теорема 1. (Кантора) Непрерывная на отрезке является равномерно непрерывной на этом отрезке
Дано: функция f(x) – непрерывная на [ a;b ].
Докзать: функция. f(x) — равномерно непрерывная на [ a;b ].
► Доказательство проведем методом от противного. Пусть f(x) не является равномерно непрерывной на [ a;b ], т.е. $ ε * > 0 такое, что "δ >0 и для любых x’ , x” Î[ a;b ], удовлетворяющих неравенству | x’ – x” |<  , выполняется неравенство | f(x’) – f(x”) |≥
, выполняется неравенство | f(x’) – f(x”) |≥  *.
*.
Для δ = 1 $ x1’ , x1” Î[ a , b ] такие, что | x1’ – x1” |<1, выполняется неравенство
| f(x1’) – f(x1”) |≥  *.
*.
Для δ =  1 $ x2’ , x2” Î[ a , b ] такие, что | x2’ – x2” |<
1 $ x2’ , x2” Î[ a , b ] такие, что | x2’ – x2” |<  , выполняется неравенство
, выполняется неравенство
| f(x2’) – f(x2”) |≥  *.
*.
Для δ = 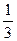 $ x3’ , x3” Î[ a , b ] такие, что | x3’ – x3” |<
$ x3’ , x3” Î[ a , b ] такие, что | x3’ – x3” |< 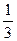 , выполняется неравенство
, выполняется неравенство
| f(x3’) – f(x3”) |≥  *.
*.
......................................................................................
Для δ =  $ xn’ , xn” Î[ a , b ] такие, что | xn’ – xn” |<
$ xn’ , xn” Î[ a , b ] такие, что | xn’ – xn” |<  , (1)
, (1)
выполняется неравенство | f(xn’) – f(xn”) |≥  *. (2)
*. (2)
......................................................................................
Таким образом на [ a , b ] построили две ограниченные последовательности (xn’), ( xn”) Þ(по Т §) $  – сходящаяся подпоследовательность последовательности (xn’), и пусть
– сходящаяся подпоследовательность последовательности (xn’), и пусть  Î[ a , b ]. (3) Адпаведная подпоследовательность
Î[ a , b ]. (3) Адпаведная подпоследовательность 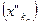 последовательности (xn”) является абмежаванайÞ$
последовательности (xn”) является абмежаванайÞ$  – збежная подпоследовательность последовательности
– збежная подпоследовательность последовательности 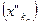 Þ
Þ 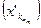 – збежная подпоследовательность последовательности
– збежная подпоследовательность последовательности  и
и  . Из неравенства
. Из неравенства
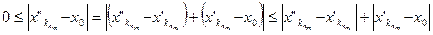
по теореме о пределе промежуточной последовательности, с учетом (1) и (3), получаем, что  Î[ a , b ]. По условию теоремы функция f(x) –непрерывна на [ a;b ], а значит и в точке х0. Воспользуемся определением непрерывной функции по Гейне:
Î[ a , b ]. По условию теоремы функция f(x) –непрерывна на [ a;b ], а значит и в точке х0. Воспользуемся определением непрерывной функции по Гейне: 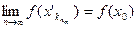 ,
, 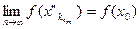 Þ
Þ  Þ" ε >0 (а значит и для ε =
Þ" ε >0 (а значит и для ε =  *.) $ n0 ÎN такой, что " n > n0, n ÎN выполняется неравенство
*.) $ n0 ÎN такой, что " n > n0, n ÎN выполняется неравенство 
 *, что противоречит (2). Полученное противоречие доказывает теорему.◄
*, что противоречит (2). Полученное противоречие доказывает теорему.◄
Следствие. Если функция f (x) непрерывна на [ a, b ], тогда 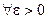
 такое, что при любом делении [ a,b ] на части точками a = x 0< x 1<… < xk –1< xk <… xn = b, при условии, что длины отрезков деления меньше
такое, что при любом делении [ a,b ] на части точками a = x 0< x 1<… < xk –1< xk <… xn = b, при условии, что длины отрезков деления меньше  , выполняется неравенство
, выполняется неравенство
 .
.
Замечание. Если функция f (x) непрерывна на (a, b), то теорема Кантора, вообще говоря, не имеет места.
Пример 3. Функция  не является равномерно непрерывной на (0;1). Действительно, для " ε >0 $ δ = min
не является равномерно непрерывной на (0;1). Действительно, для " ε >0 $ δ = min 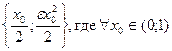 такое, что " х Î(0;1), удовлетворяющие условию | x – x 0|<
такое, что " х Î(0;1), удовлетворяющие условию | x – x 0|<  , выполняется неравенство | f (x) – f (x 0)|<
, выполняется неравенство | f (x) – f (x 0)|<  — это определение непрерывной в любой точке
— это определение непрерывной в любой точке 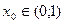 функции по Коши. Из формулы для δ видно, что оно зависит от x 0 Пакажем, что " ε >0 нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1) и, как только | x – x 0|<
функции по Коши. Из формулы для δ видно, что оно зависит от x 0 Пакажем, что " ε >0 нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1) и, как только | x – x 0|<  , то выполняется неравенство | f (x) – f (x 0)|<
, то выполняется неравенство | f (x) – f (x 0)|<  . Доказательство проведем методом от противного, пусть для ε >0
. Доказательство проведем методом от противного, пусть для ε >0  такое, что
такое, что 
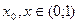 , удовлетворяющих условию | x 0– x |<
, удовлетворяющих условию | x 0– x |<  , выполняется неравенство | f(x0) – f(x) |< ε. Возьмем 0< x0 <δ, а потом 0< x <
, выполняется неравенство | f(x0) – f(x) |< ε. Возьмем 0< x0 <δ, а потом 0< x <  Þ
Þ
Þ  , но f (x) – f (x 0)=
, но f (x) – f (x 0)=  (противоречие) Þ нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1).
(противоречие) Þ нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1).
Определение 2. Величина  называется колебанием функции f (x) на промежутке X.
называется колебанием функции f (x) на промежутке X.

 и пакажем, что найдется такое
и пакажем, что найдется такое  , что для всех
, что для всех 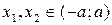 , удовлетворяющих неравенству | x 1– x 2|<
, удовлетворяющих неравенству | x 1– x 2|<  , выполняется неравенство
, выполняется неравенство . Рассмотрим разность
. Рассмотрим разность , то модуль суммы
, то модуль суммы | x 1– x 2|<
| x 1– x 2|< 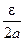 . Тогда для всех
. Тогда для всех  , удовлетворяющих условию | x 1– x 2|<
, удовлетворяющих условию | x 1– x 2|< 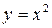 равномерно непрерывная на интервале (– a;a), по определению.
равномерно непрерывная на интервале (– a;a), по определению. не является равномерно непрерывной на всей числовой прямой.
не является равномерно непрерывной на всей числовой прямой. , такие, что| x 1– x 2|<
, такие, что| x 1– x 2|< 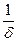 +
+  и x 2 =
и x 2 =  –любое положительное число, они удовлетворяют неравенству
–любое положительное число, они удовлетворяют неравенству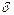 , но | x 12– x 22| = | x 1– x 2|| x 1+ x 2|=
, но | x 12– x 22| = | x 1– x 2|| x 1+ x 2|=  (
(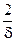 +
+ 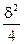 ≥1. Значит
≥1. Значит  1 $ x2’ , x2” Î[ a , b ] такие, что | x2’ – x2” |<
1 $ x2’ , x2” Î[ a , b ] такие, что | x2’ – x2” |< 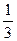 $ x3’ , x3” Î[ a , b ] такие, что | x3’ – x3” |<
$ x3’ , x3” Î[ a , b ] такие, что | x3’ – x3” |<  $ xn’ , xn” Î[ a , b ] такие, что | xn’ – xn” |<
$ xn’ , xn” Î[ a , b ] такие, что | xn’ – xn” |<  – сходящаяся подпоследовательность последовательности (xn’), и пусть
– сходящаяся подпоследовательность последовательности (xn’), и пусть  Î[ a , b ]. (3) Адпаведная подпоследовательность
Î[ a , b ]. (3) Адпаведная подпоследовательность 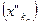 последовательности (xn”) является абмежаванайÞ$
последовательности (xn”) является абмежаванайÞ$  – збежная подпоследовательность последовательности
– збежная подпоследовательность последовательности 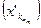 – збежная подпоследовательность последовательности
– збежная подпоследовательность последовательности  . Из неравенства
. Из неравенства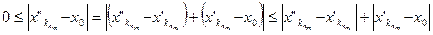
 Î[ a , b ]. По условию теоремы функция f(x) –непрерывна на [ a;b ], а значит и в точке х0. Воспользуемся определением непрерывной функции по Гейне:
Î[ a , b ]. По условию теоремы функция f(x) –непрерывна на [ a;b ], а значит и в точке х0. Воспользуемся определением непрерывной функции по Гейне: 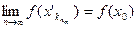 ,
, 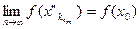 Þ
Þ  Þ" ε >0 (а значит и для ε =
Þ" ε >0 (а значит и для ε = 
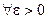
 такое, что при любом делении [ a,b ] на части точками a = x 0< x 1<… < xk –1< xk <… xn = b, при условии, что длины отрезков деления меньше
такое, что при любом делении [ a,b ] на части точками a = x 0< x 1<… < xk –1< xk <… xn = b, при условии, что длины отрезков деления меньше  .
. не является равномерно непрерывной на (0;1). Действительно, для " ε >0 $ δ = min
не является равномерно непрерывной на (0;1). Действительно, для " ε >0 $ δ = min 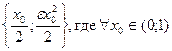 такое, что " х Î(0;1), удовлетворяющие условию | x – x 0|<
такое, что " х Î(0;1), удовлетворяющие условию | x – x 0|< 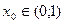 функции по Коши. Из формулы для δ видно, что оно зависит от x 0 Пакажем, что " ε >0 нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1) и, как только | x – x 0|<
функции по Коши. Из формулы для δ видно, что оно зависит от x 0 Пакажем, что " ε >0 нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1) и, как только | x – x 0|<  такое, что
такое, что 
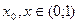 , удовлетворяющих условию | x 0– x |<
, удовлетворяющих условию | x 0– x |<  Þ
Þ , но f (x) – f (x 0)=
, но f (x) – f (x 0)=  (противоречие) Þ нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1).
(противоречие) Þ нельзя подобрать δ такое, чтобы оно было одинаковым для всех х0 Î(0;1). называется колебанием функции f (x) на промежутке X.
называется колебанием функции f (x) на промежутке X.


