Передача винт – гайка.Основное назначение передач типа «винт — гайка» — преобразование вращательного движения в поступательное. Эти передачи бесшумны в работе, что достигается повышенной плавностью зацепления, просты по конструкции и в изготовлении и позволяют получать большой выигрыш в силе. К недостаткам следует отнести: относительно низкий КПД, склонность к заеданию, тихоходность передачи. Передачи типа «винт — гайка» применяют в подъемных механизмах, в станках (механизмы подачи рабочих инструментов), в измерительных приборах (механизмы для точных перемещений, микрометрические и дифференциальные винты), в прокатных станах (регулировочно-установочные механизмы подшипников, нажимные винты), в винтовых процессах.
Рис.
Пространственная кинематическая винтовая пара «винт – гайка» (рис.)обладает следующим свойством: при неподвижном винте 2 поворот гайки 1 на один поворот вызывает ее перемещение вдоль оси винта на величину хода; если закрепить гайку и повернуть винт на один поворот, то, помимо вращения, винт переместится вдоль оси на величину хода. Винтовые механизмы принципиально ничем не отличаются от резьбовых соединений, но так как они применяются для передачи движения, то трение в резьбе должно быть минимальным. Наименьшее трение между винтом и гайкой обеспечивает прямоугольная резьба, однако ее нетехнологичность, то есть невозможность нарезания на резьбофрезерных станках, и небольшая прочность по сравнению с трапецеидальной резьбой делают ее применение крайне ограниченным. Поэтому для передаточных винтов применяют главным образом трапецеидальную резьбу с мелким, средним и крупным шагами и упорную резьбу. Наибольшее распространение получила трапецеидальная резьба со средним шагом. Трапецеидальную резьбу с мелким шагом используют при относительно небольших перемещениях; трапецеидальную резьбу с крупным шагом — при тяжелых условиях эксплуатации. Профиль трапецеидальной резьбы позволяет использовать ее в механизмах с реверсивным перемещением. Для передач с большими односторонними нагрузками (прессы, домкраты, нажимные устройства в прокатных станах и др.) применяют упорную резьбу. Резьба винтов и гаек передач бывает правой или левой, однозаходной или многозаходной. Материалы винтов должны обладать высокой износостойкостью и хорошей обрабатываемостью, а более нагруженные — высокой прочностью. Винты, не подвергаемые закалке, изготовляют из сталей 45, 50, А50, а винты, подвергаемые закалке, выполняют из сталей У10, У65, 40Х, 40ХГ и др. Материал гаек— бронзы оловянные БрОФЮ- 1, БрОЦС-6-6-3 и др. Интенсивное развитие технологии предъявляет особые требования к механизмам линейного перемещения промышленного оборудования. Из всего многообразия конструкций передач винт-гайка наиболее известны шарико-винтовые передачи (ШВП) (рис. 2). Существенные недостатки передач скольжения – низкий КПД, нестабильность момента трения, быстрый износ, что ограничивают область их применения, а наличие канала возврата шариков в ШВП ограничивает предельную частоту вращения ходового винта Канавки шарикового винта 3 (рис. 166, I) и гайки 2 в осевом сечении имеют полукруглую форму. Непрерывный замкнутый поток шариков 4 заполняет винтовое пространство между желобами по всей длине гайки. Пройдя его, шарики переходят в округленный трубчатый канал 1, по которому они возвращаются в рабочую зону винтовой пары. Канавки шарикового винта 3 (рис., I) и гайки 2 в осевом сечении имеют полукруглую форму. Непрерывный замкнутый поток шариков 4 заполняет винтовое пространство между желобами по всей длине гайки. Пройдя его, шарики переходят в округленный трубчатый канал 1, по которому они возвращаются в рабочую зону винтовой пары.
Коэффициент полезного действия шариковой винтовой пары много выше, чем обычной, вследствие резкого снижения трения в резьбе. Для полного устранения зазоров в шариковой паре «винт — гайка» на винте устанавливают одновременно две шариковые гайки 2 (рис., II), между которыми помещают стальную пружину 5. Пружина, создавая предварительный натяг между винтом 3, шариками и гайками, устраняет все зазоры в передаче. Интенсивное развитие технологии предъявляет особые требования к механизмам линейного перемещения промышленного оборудования. Существенными недостатками передач винт-гайка являются: передачи скольжения – низкий КПД, нестабильность момента трения, быстрый износ – ограничивают область их применения; ШВП - наличие канала возврата шариков ограничивает предельную частоту вращения ходового винта. Ролико-винтовая передача представляет собой механизм преобразования вращательного движения в поступательное, аналогично тому, как это происходит в традиционных передачах типа ШВП или с трапецеидальной резьбой. Однако в отличие от этих устройств, ролико-винтовая пара может выдерживать большие нагрузки в течение тысяч часов эксплуатации в самых жестких условиях. В связи с этим ролико-винтовая пара идеально подходит для ответственных применений с непрерывным режимом работы.
Рис.1;2
Качественные отличия ролико-винтовой передачи и ШВП.
В традиционной конструкции шарико-винтовой пары вал электродвигателя жестко соединен с резьбовым валом шарико-винтовой передачи. В следствие вращения вала, каретка, находящаяся на валу начинает двигаться поступательно. Каретка, в свою очередь, закреплена таким образом, чтобы не проворачиваться. Для уменьшения сил трения, между кареткой и резьбовым валом пускаются металлические шарики, чтобы избежать трения скольжения. 1) При движении каретки, момент электродвигателя передается посредством контакта шариков с резьбовым валом и кареткой. Чем меньше точек контакта, тем меньше максимальная нагрузка и долговечность.
Пример приложения нагрузки:
Данный рисунок показывает, что в сходных габаритах, ШВП и ролико-винтовой передачи (РВП), точек контакта значительно больше у последней. А значит намного больше нагрузочная способность и ресурс. 2) Более низкий КПД и максимальная скорость у шарико-винтовой пары обусловленна следующими факторами:
Чем больше скорость, тем больше трение и износ шариков, что уменьшает КПД.
шариков, поэтому, все, даже самые точные и дорогии ШВП не рассчитаны на скорости свыше 2000 об/мин. Конструкция РВП лишена подобных недостатков. Все ролики жестко закреплены друг от друга и не могут соприкасаться. Для механической синхронизации вращения каждого ролика применены специальные зубчики на конце роликов, что позволяет избегать ненужных проскальзываний. Сравнение ролико-винтовых и шарико-винтовых передач. - очень высокими допустимыми ускорениями (7000 рад/сек2); - долгим сроком службы даже при постоянной работе; - хорошей сопротивляемостью агрессивным средам (пыль, песок, лёд); - хорошей сопротивляемостью ударным нагрузкам и вибрациям;
Планетарная передача.
Планетарными передачами называются механические передачи вращения, некоторые колеса которых не только вращаются относительно собственной оси, но и параллельно перемещаются в пространстве. Под перемещением понимается вращение относительно центрального колеса, которое называется центральным, или солнечным. Колеса с подвижными осями называются сателлитами и вращаются относительно центральной оси подобно спутникам, которые перемещаются относительно Солнца. Такая аналогия дала название этой группе механизмов — планетарные. Сателлиты при вращении удерживаются в требуемом положении в подвижном корпусе, который называют водилом. Таким образом, планетарным называют механизм, состоящий из зубчатых колес, в котором геометрическая ось, хотя бы одного из колес подвижна. Планетарный редуктор имеет тип передачи, который относится к зубчатым передачам с непосредственным контактом тел вращения. Это передачи вращательного движения и служат для передачи энергии от двигателей к рабочим машинам, с преобразованием скоростей, сил и крутящих моментов. Основные элементы планетарной передачи следующие: - солнечная шестерня, находится в центре (1); - водило, жёстко фиксирует друг относительно друга оси нескольких планетарных шестерён (сателлитов) (2) одинакового размера, находящихся в зацеплении с солнечной шестерней (Н); - кольцевая шестерня (эпицикл): внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями (3). Одно из центральных колес планетарной передачи установлено неподвижно. Ведущим (или ведомым) валом передачи служит вал подвижного центрального колеса, а ведомым (или ведущим) — вал водила.
Планетарная передача
Рис. Планетарные передачи: а) конструктивная схема; б) – кинематическая схема передачи.
Простая планетарная передача включает центральные колеса с внешними и внутренними зубьями ( Принцип работы планетарных передач: при закрепленном колесе Основными звеньями планетарной передачи называют такие, которые воспринимают внешние моменты. На схеме а ведущими являются два центральных колеса и водило (сокращенно обозначают 2К-h). Любое основное звено планетарной передачи может быть остановлено Если в планетарной передаче сделать подвижными все звенья, т. е., оба колеса и водило, то такую передачу называют дифференциалом. С помощью дифференциала одно движение можно разложить на два или два сложить в одно. Например, движение от колеса a можно передавать одновременно колесу b и водилу h или от колес b и a водилу h и т. д.
а б Рис. Принципиальная схема дифференциальной передачи: а, б) – дифференциальные передачи (суммирующая и раскладывающая скорости вращения). Здесь показано суммирование движений звена На схеме (б) показан дифференциал заднего колеса автомобиля. Водило получает вращение от конической передачи
В планетарных передачах применяются не только цилиндрические, но и конические колеса. Зубья в планетарных передачах могут быть прямые и косые. Планетарные редукторы имеют гораздо больше положительных свойств, а значит значительно выгоднее, чем редукторы цилиндрические.
К достоинствам планетарных передач относят: 1. малые габариты и масса (передача вписывается в размеры внешнего колеса). Это объясняется тем, что мощность передается по нескольким потокам, численно равным числу сателлитов, поэтому нагрузка на зубья в каждом зацеплении уменьшается в несколько раз. В то же время планетарные редукторы могут иметь значительные передаточные отношения в одной ступени по сравнению с другими типами редукторов, что позволяет не прибегать к сложным многоступенчатым передачам. Передачи с внутренним зацеплением, обладают повышенной несущей способностью; они обладают малой удельной материалоемкостью при достаточно большой нагрузочной способности. Также отличительными чертами таких редукторов являются высокая степень надежности работы 2. удобство компоновки машин благодаря соосности ведущих и ведомых валов. 3. меньший шум, чем в обычных зубчатых передачах, что связано с меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. 4. малые нагрузки на опоры, что упрощает конструкцию опор и снижает потери в них. 5. планетарный принцип передачи движения позволяет получить большие передаточные числа при небольшом числе зубчатых колес и малых габаритах. К недостаткам передач можно отнести: 1. повышенную точность изготовления; 2. большое число подшипников качения; 3.снижение к.п.д. передачи с ростом передаточного числа. Наиболее распространенные схемы передач имеют либо высокие КПД, либо большие передаточные отношения. При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, другой элемент используется как ведущий, а третий — в качестве ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также того, какой элемент закреплён. Передаточное отношение обозначают буквой с индексами, например .Как известно из теории механизмов, передаточное отношение планетарных механизмов удобнее всего определять, мысленно сообщив всей системе переносное движение с угловой скоростью, равной скорости водила, но обратной по знаку. Тогда получим механизм с остановленным водилом, т.е. так называемый приведенный механизм, который является непланетарным. Для этого механизма записывают выражение передаточного отношения через угловые скорости звеньев относительно водила (уравнение Виллиса):
где Передаточное отношение считается положительным, если в приведенном механизме входные и выходные звенья вращаются в одну сторону (внутреннее зацепление), и отрицательным – если в разные стороны (внешнее зацепление).
Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S, а для планетарных шестерён примем это число как P, то передаточное отношение будет определяться формулой − S / P, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет -24/16, или -3/2, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной. Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A зубьев, то оно будет вращаться с соотношением P / A относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 16/64, или 1/4. Таким образом, объединив оба примера, мы получим следующее: - один оборот солнечной шестерни даёт - S / P оборотов планетарных шестерён; - один оборот планетарной шестерни даёт P / A оборотов кольцевой. В итоге, если водило заблокировано, общее передаточное отношение системы будет равно - S / A. В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет больше единицы и составит 1+ A / S. Всё вышесказанное можно описать следующим выражением:
где n — это параметр передачи, равный Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно 1 / (1 + A / S). Это самое маленькое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.
Особенности расчета планетарных передач. В отличие от обычных зубчатых передач расчет начинают с выбора чисел зубчатых колес. Так как колеса взаимосвязаны, то кроме обеспечения заданного передаточного отношения необходимо удовлетворить следующим условиям сборки: соосности, симметричного расположения сателлитов, соседства. Условие соосности требует равенства межосевых расстояний различных пар зацепляющихся колес. Условие симметричного расположения сателлитов, чтобы число зубьев центральных колес было кратно числу сателлитов. Условие соседства обязывает иметь такие размеры сателлитов, чтобы они не задевали друг друга. Расчеты на прочность и на выносливость зубьев при изгибе проводят для обращенного механизма (при остановленном водиле) по формулам для расчета зубчатых передач. Разновидности планетарных передач Существует большое количество различных типов планетарных передач. Выбор типа передачи определяется ее назначением. Наиболее широко в машиностроении применяется однорядная планетарная передача. Это передача имеет минимальные габариты. Применяется в силовых и вспомогательных приводах. К.п.д. передачи равно 0,96...0,98 при передаточных числах = 3,15...12,5. Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. Подбор чисел зубьев планетарных передач На практике наибольшее распространение получила планетарная однорядная прямозубая передача, расчет которой и рассматривается ниже. Числом зубьев центральной шестерни задаются из условия неподрезания ножки зуба, принимая для нее z1>17. Число зубьев неподвижного колеса 3 определяют по заданному передаточному числу из формулы: z3 = z1(и-1). Число зубьев сателлитов вычисляют из условия соосности, по которому межосевые расстояния аw зубчатых пар с внешним и внутренним зацеплениями должны быть равны. Для кекорригированной прямозубой передачи аw = 0,5(d1+d2)=0,5(d3-d2), где d=mz -- делительные диаметры. Так как модули зацеплений планетарной передачи одинаковые, то Z2 = 0,5(z3 - z1). Полученные числа зубьев z1, z2 и z3 проверяют по условиям сборки и соседства. Условие сборки требует, чтобы во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу невозможно. Установлено, что при симметричном расположений сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z1+ z3) кратна числу сателлитов с=2...6 (обычно с = 3), т.е. (z1+ z3)/с = целому числу. Условие соседства требует, чтобы сателлиты при вращении не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная da2=m (Z2+2), была меньше расстояния между их осями, т. е. da2<l = 2aw sin п/с,) где aw = 0,5m (z1+ z2) - межосевое расстояние. От сюда следует, что условие соседства удовлетворяется, когда z2+2<(z1+ z2) sin п/с. Расчет на прочность планетарных передач Расчет на прочность зубьев планетарных передач ведут по формулам обыкновенных зубчатых передач. Расчет выполняют для каждого зацепления. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочней внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление. При определении допускаемых напряжений коэффициенты долговечности Кhl и Kfl находят по числу циклов N' перемены напряжений зубьев за весь срок службы при вращении колес только относительно друг друга. Для центральной шестерни N'=573сw'1Lh где w'1=w1--wн-- относительная угловая скорость центральной шестерни; w1 и wн -- угловые скорости центральной шестерни и водила. Для сателлитов N2'=573w'2Lh где w'2=w'1z1/z2а -- относительная угловая скорость сателлита. Межосевое расстояние планетарной прямозубой передачи пары колес внешнего зацепления (центральной шестерни с сателлитом) определяют по формуле: аw>49,5(u' +1) КсТ1/сфа u'Кнв где u'=z2/z1 -- передаточное число рассчитываемой пары колес; Кс=1,1...1,2 -- коэффициент неравномерности распределения нагрузки между сателлитами; Т1 -- вращающий момент на валу центральной шестерни, Н*мм; фа - коэффициент ширины венца колеса. При и'<6,3 принимают фа=0,5, а при u'>6,3 фa=0,4. Полученное значение aw округляют до стандартного значения. Ширина центрального (корончатого) колеса B3= фaaw. (13) Ширину венцов сателлитов и центральной шестерни принимают на 2...4 мм больше значения B3 Делительный диаметр центральной шестерни d1=2aw/ u+1 Модуль зацепления m= d1/z1 Полученный расчетом модуль округляют до ближайшего стандартного значений, а затем уточняют числа колес по формулам: Z1=2aw/m(u'+1) Z2= Z1 u', Z3=z1+2z2 с последующей проверкой условий сборки и соседства. Окружную силу в зацеплении вычисляют по формуле Ft=2КС Т1/сd1 Радиальную силу определяют, как в обычных передачах. Конструктивные особенности планетарных передач Вследствие неизбежной неточности изготовления нагрузка между сателлитами распределяется неравномерно. Для выравнивания нагрузки по потокам в передачах с тремя сателлитами одно из центральных колес делают самоустанавливающимся в радиальном направлении (не имеющим радиальных опор). Для самоустановки сателлитов по неподвижному центральному колесу применяют сферические подшипники качения. Водила планетарных передач должны быть прочными и жесткими при малой массе. Выполняют их литыми из высокопрочного чугуна марки ВЧ50-2 часто за одно целое с тихоходным валом или сварными. Выбор типоразмера планетарного редуктора, мотор-редуктора Выбор типоразмера планетарного редуктора производится по таблице технических характеристика. Рассчитывают требуемое передаточное отношение редуктора: iР = n1p/n2р, (1) где: Определяют расчётно-эксплуатационное значение крутящего момента T2РЭ на выходном валу: T2РЭ= ТРАСЧ · КЭ (2) где: КЭ = К1 · К2 · К3 · К4 · К5 (3) Значения коэффициентов К1 – К5 выбираются по таблицам 1 – 5, исходя из фактических условий и режимов эксплуатации редуктора. По таблице технических характеристик редуктора: - сравнивают расчетное значение передаточного отношения с табличными и находят ближайшее меньшее iM и ближайшее большее значение iБ для найденных iM и iБ: - сравнивают табличные значения частот вращения валов редуктора n1 и n2 с их исходными (требуемыми) значениями; - сравнивают табличные значения передаваемых моментов; - из двух значений iM и iБ выбирают передаточное отношение i редуктора в зависимости от наиболее значимых конструкторско-эксплуатационных факторов, таких как: - минимум отклонения от требуемого значения параметра n2; - максимум передаваемого момента; - для выбранного значения i сравнивают табличные значения Т2 с расчетным значением Т2РЭ и находят: ближайшее меньшее значение крутящего момента Т2М; ближайшее большее значение крутящего момента Т2Б; определяют: - типоразмер редуктора, соответствующий ближайшему меньшему значению крутящего момента Т2М; - типоразмер редуктора, соответствующий ближайшему большему значению крутящего момента Т2Б. Сравнивают технико-эксплуатационные показатели, габариты и массу редукторов и производят дополнительный конструктивно-эксплуатационный анализ в целях определения возможности выбора редуктора ближайшего меньшего типоразмера. Для этого пересматривают конструкцию машины (условия и режимы ее эксплуатации) в целях уменьшения значения эксплуатационного коэффициента КЭ и, соответственно, уменьшения расчетно-эксплуатационного момента Т2РЭ до значения Т2РЭ меньше или равно Т2. Таблица 1 — Коэффициент режима эксплуатации К1
Таблица 2 — Температурный коеффициент К2
Таблица 3 — Коэффициент смазки К3
Таблица 4 — Коэффициент наличия упругих элементов К4
Таблица 5 — Коэффициент реверсивних пусков К5
.
|
). По центральным колесам обкатываются сателлиты (
) с внешними зубьями, оси которых расположены в водиле (
). На схеме водило соединено с тихоходным валом, 
- числа зубьев колес, 
- число сателлитов (в нашем случае их 3).
(
) вращение колеса 
(
вызывает вращение сателлита 
. Качение сателлита по 
. Вращение сателлита напоминает движение планет, поэтому передача называется планетарной.
и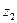 
. Вращение водила раскладывается между колесами 
. Нижние индексы обозначают направление передачи движения, верхний индекс определяет звено, обычно неподвижное, относительно которого рассматривается движение; если направления вращения ведущего и ведомого звеньев одинаковы, то передаточное отношение считается положительным, если различны — отрицательным.
,
- частота вращения основных звеньев, 
.
.
, то есть отношению числа зубьев солнечной и планетарных шестерён.
