Уравнение связи осевой и окружной составляющих скорости
Чтобы установить изменение скорости потока по высоте лопаток, надо из уравнения радиального равновесия исключить величину давления. Для этого запишем уравнение сохранения энергии для струйки тока в осевом зазоре перед РК. Механическая работа в зазоре не совершается (
В такой форме оно справедливо только вдоль поверхности (струйки) тока. Если принять допущение, что процесс изменения состояния для всех струек протекает по одной и той же политропе, то уравнение можно продифференцировать по радиусу Подставим значение Поскольку Последнее уравнение даёт связь между скоростью потока в элементарной ступени и радиусом, на котором эта элементарная ступень расположена. Но в него входят две неизвестные величины – - закон постоянной циркуляции - закон постоянной реактивности - закон твёрдого тела
|
), потерями пренебрегаем (
), индексы 1 и 2 соответствуют входу в осевой зазор и выходу из него.
из уравнения радиального равновесия, получим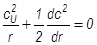 
.
, то 
(2)
и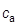 
. Поэтому для его решения одна из переменных должна быть задана. В лопаточных машинах обычно задаются законом изменения 
. Такие зависимости называются законами закрутки. Чаще всего используют:
;
;
.
