Геометрические особенности фасонных резцов
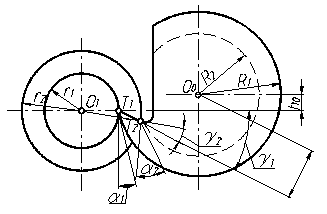
Фасонные резцы, так же как и обычные (проходные, подрезные и т.д.), должны иметь соответствующие передние и задние углы, чтобы обеспечить рациональные углы резания. Причем все, что касается передних и задних углов обычных резцов, целиком может быть перенесено и на фасонные резцы. Задний угол круглого фасонного резца образуется за счет установки оси резца выше оси обрабатываемой детали на величину h0 (см. рис. 2.1): h0=R1·sin(α1) (2.1.) где R1 - радиус резца для точки Т1; α1- задний угол для точки Т1. Передний угол круглого фасонного резца образуется в процессе заточки. Для этого переднею грань резца опускают ниже его оси на величину Н0: Н0=R1·sin(γ1+ α1) (2.2) где R1 - радиус резца для точки Т1; γ1 - передний угол для точки Т1.
Рис. 2.1. Задний угол призматического фасонного резца достигается наклонной установкой тела резца под этим углом к плоскости резания (см. рис. 2.2). Передний угол образуется заточкой передней поверхности под углом β к образующей задней поверхности. Угол β определяется по формуле: β=90˚- (α1 + γ1) (2.3) Характерной особенностью фасонных резцов является то, что передние и задние углы у них для различных точек профиля неодинаковы. Покажем это на примере призматического фасонного резца (см. рис. 2.2). Для этого продолжим линию передней поверхности и опустим перпендикуляр из центра детали (точки О1) на эту линию. Точку пересечения перпендикуляра с линией передней поверхности обозначим буквой К. Из рассмотрения треугольников Т1КО1 и Т2КО1 следует, что O1К=r1·sin(γ1) и O1К=r2·sin(γ2) (2.4) Тогда r1·sin(γ1)= r2·sin(γ2), и, следовательно, sin(γ2)=(r1/r2) ·sin(γ1) (2.5)
Рис. 2.2. Схема, иллюстрирующая изменение геометрических параметров призматического фасонного резца Кроме того, из того, что r1>r2, следует выполнение следующих неравенств:
При х<π/2, функция sin(x) является непрерывно возрастающей. Тогда для технологически допустимых значении переднего угла γ (γ <<π/2) из неравенств (2.6.) следует неравенство γ2< γ1. Таким образом, можно утверждать, что передний угол изменяется по длине режущей кромки фасонного резца, причем участки режущей кромки, обрабатывающие поверхности большего диаметра, имеют меньшие значения переднего угла. Для анализа величин задних углов в различных точках профиля через точки Т1 и Т2 проведем линии, перпендикулярные к образующим задних поверхностей в этих точках. Из построения следует, что ψ1= α1 + γ1 и ψ2= α2 + γ2 (2.7) Принимая во внимание равенство ψ1 = ψ2 можно записать: α2= α1+(γ1- γ2) (2.8) Как установлено ранее γ1>γ2, следовательно, (γ1- γ2)>0. Тогда из (2.8) следует неравенство задних углов в точка Т1 и Т2, то есть выполняется условие α1> α2. Аналогичный результат может быть получен и для круглых фасонных резцов. Таким образом, применительно к фасонным резцам можно сделать следующий вывод: у фасонных резцов (как круглых так и призматических) с приближением рассматриваемых точек режущей кромки к центру или базе крепления резца передние утлы непрерывно уменьшаются, а задние непрерывно возрастают. Выше мы рассматривали геометрические параметры фасонных резцов (передние и задние углы) в радиальной плоскости (плоскости, перпендикулярной к оси заготовки). Однако очень часто участки режущей кромки фасонного резца располагаются не параллельно, а под углом к оси обрабатываемой детали. В этих случаях условия резания и жесткость резца зависит не от радиальных углов, а от значения передних и задних углов в сечении, перпендикулярном проекции режущей кромки на основную плоскость. На рис. 2.3 представлена схема определения заднего угла в сечении, нормальном к проекции режущей кромки на основную плоскость в произвольной точке Т1 на участке кромки, расположенном под углом к оси детали. Построения проводятся применительно к призматическому фасонному резцу. Плоскость А-А - радиальная (перпендикулярная оси детали) плоскость, a - задний угол в радиальном сечении. Сечение Б-Б соответствует главной секущей плоскости, α - искомый задний угол.
Рис. 2.3. Схема определения величин заднего угла в нормальном сечении Из схемы, приведенной на рис. 2.3, следует, что
Аналогичным образом может быть получена формула для определения переднего угла в главной секущей плоскости:
При проектировании фасонных резцов особое внимание следует уделить правильному выбору заднего угла. При обработке фасонными резцами часто встречаются профили, отдельные участки которых располагаются радиально, то есть на этих участках углы в плане φ Несмотря на принимаемые меры, износ фасонных резцов на участках режущих кромок, перпендикулярных оси детали,протекает в несколько раз интенсивнее, а качество обработанной поверхности бывает гораздо хуже, чем на других участках режущей кромки. Если же детали, обрабатываемые фасонными резцами ХХХХ поверхности, расположенные радиально, и требуется точная их обработка с малой шероховатостью, то для изготовления таких деталей необходимо проектировать фасонные резцы с винтовыми образующими фасонных поверхностей или с наклонными расположением оси или базы крепления.
Рис. 2.4. Мероприятия по улучшению задних углов фасонных резцов
Корректно спроектированные и точно изготовленные фасонные резцы при правильной их установке на станках обеспечивают точность формы и размеров обрабатываемых деталей по IT8…IT12 и шероховатость обработанной поверхности на уровне Ra – 0,62…2,5 мкм [14, с.126].
|


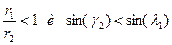 (2.6)
(2.6)
 ;
;  , где Н – высота резца. Так как
, где Н – высота резца. Так как  , где φ - угол в плане для рассматриваемого участка режущей кромки, можем записать:
, где φ - угол в плане для рассматриваемого участка режущей кромки, можем записать: (2.9)
(2.9) (2.10)
(2.10) Величина его должна быть, такой, чтобы для самой неблагоприятной точки режущей кромки (точки, для которой угол в плане является максимальным), обеспечить задний гол в главной секущей плоскости не менее 2-3°. Если по 1 счету, эти углы получаются меньше, то задний угол на вершине резца должен быть увеличен (однако не допускается назначение заднего угла на вершине более 15°).
Величина его должна быть, такой, чтобы для самой неблагоприятной точки режущей кромки (точки, для которой угол в плане является максимальным), обеспечить задний гол в главной секущей плоскости не менее 2-3°. Если по 1 счету, эти углы получаются меньше, то задний угол на вершине резца должен быть увеличен (однако не допускается назначение заднего угла на вершине более 15°).



