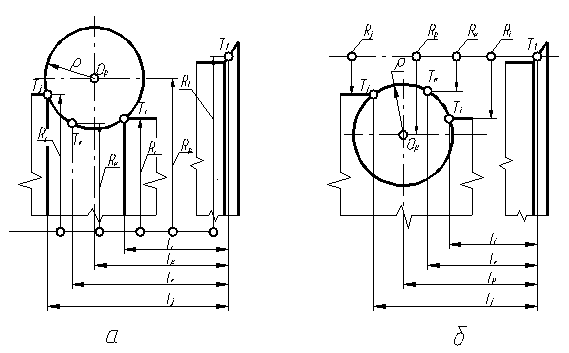
Построение радиусных участков профиля резца
Необходимость в определении формы криволинейных участков профиля резца по положению ряда его точек возникает сравнительно редко. В большинстве случаев с достаточной для практики точностью кривую заменяют дугой окружности. Так, в частности, дугой окружности заменяют участки профиля резца, обрабатывающие участки изделия, поверхность которых представляет собой элемент сферы. Так как дуга окружности используется в данном случае длязамены кривой второго порядка, такая окружность называется «заменяющей». Задача построения заменяющей окружности является обратной по отношению к задаче определения промежуточной узловой точки, криволинейного участка. При построении заменяющей окружности требуется определить координаты ее центра (для круглого резца - lр; для призматического резца - Rр) и радиус ρ по координатам трех узловых точек окружности. Так как в задаче имеются три неизвестных, требуется решение системы трех уравнений. Схема к решению задачи построения заменяющей окружности представлена на рис. 4.7. Последовательность вычислений сведется к следующей последовательности шагов; 1. Выделить узловые точки Тi, Тк, Тjучастка профиля инструмента, который обрабатывает криволинейный участок профиля детали, и определить их координаты в системе координат, связанной с инструментом. Координаты любой точки Тi, профиля инструмента для круглого фасонного резца определяются парой значений (li; Ri), для призматического резца - парой значений (li; Pi). 2. На основе уравнения окружности (4.4) составить систему трех уравнений с тремя неизвестными. Каждое уравнение является условием, принадлежности одной из узловых точек искомой заменяющей окружности. Тогда для круглого резца получим: для точки Тi для точки Тk для точки Тj Аналогично для призматического резца: для точки Тi для точки Тk для точки Тj 3. Подставив в полученную систему уравнений известные значения координат точек Тi, Тk, Тj разрешить ее относительно неизвестных значений: для круглого резца
4.7. Схема построения заменяющей окружности для круглого (а) и призматического (б) фасонных резцов.
Получение значения координат центра и радиуса заменяющей окружности округляются с точностью до 0,01 мм и указываются на чертеже инструмента. В случае, если требуется описание криволинейного участка профиля инструмента не другой окружности, а иной кривой линии (фрагментом параболы, гиперболы, эллипса, некоторой специальной кривой), общая процедура решения задачи не изменяется. Отличия заключаются в том, что вместо уравнения окружности (4.4) при составлении системы уравнений используется уравнение заданной кривой. Кроме того, используется количество узловых точек (уравнений системы), равное количеству независимых параметров в уравнении кривой.
|

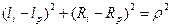 ;
; ; (4.10)
; (4.10)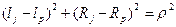 .
. ;
;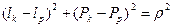 ; (4.11)
; (4.11)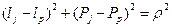 .
.