Простые линейные алгоритмы
Для каждой из нижеприведенных задач составить графическую схему алгоритма и написать программу. Данные для тестового примера выбрать самостоятельно.
Вариант 1. Определить проекцию XA точки А кривошипа на ось координат Oх по формуле XA=r∙cos φ;, где r - длина кривошипа, φ - угол поворота. Вариант 2. Определить текущую координату Х точки А ведущего звена кривошипа по формуле XA=r∙cos(ω∙t), где r - длина кривошипа, ω - угол поворота, t - время вращения. Вариант 3. Эксцентрик вращается равномерно с постоянной угловой скоростью. Вычислить инерционную нагрузку эксцентрика по формуле Pu=m∙ω2∙ε∙(cosφ – sinφ), где m -масса толкателя, ω; -частота вращения, ε; - эксцентриситет, φ-угол поворота. Вариант 4. Определить значение возмущающей силы, действующей на вибромолот по формуле F=2∙m0∙r0∙ω2, где m0 - масса эксцентрика, r0 -расстояние центра тяжести от оси вращения, ω; - частота вращения. Вариант 5. Определить плотность стержня в точке C, расположенной посередине стержня, по формуле Вариант 6. Определить межосевое расстояние в зацеплении цилиндрических прямозубых колес по формуле Вариант 7. Определить емкость сферического конденсатора по формуле
Вариант 8. Определить проекцию точки А кривошипа на ось координат Oy по формуле YA=r∙sinφ;, где r - длина кривошипа, φ - угол поворота. Вариант 9. Определить координату ведущего звена кривошипа при равномерном вращении по формуле YA=r∙sin(ω∙t), где r - длина кривошипа, ω; - угол поворота, t - время вращения. Вариант 10. Определить работу, которую необходимо совершить, что бы переместить некоторый заряд из одной точки поля в другую, по формуле A=g(φ1-φ2), где g - заряд, φ1 и φ2 - потенциалы соответствующих точек поля. Вариант 11. Определить количество теплоты, образующейся в электрических проводах при прохождении тока, по формуле Вариант 12. Определить объемную плотность свободной энергии при малых деформациях бруса по формуле Вариант 13. Определить момент инерции однородного сплошного шара относительно оси, проходящей через центр тяжести, по формуле Вариант 14. Определить реактивную силу, действующую на горящую сферическую частицу угля, свободно падающую в топке по формуле F=5∙π∙R2∙u∙K, где R - радиус дуги, u - скорость отделения продуктов сгорания, K - скорость выгорания. Вариант 15. Определить мощность электродвигателя привода перемешивающего устройства по формуле
|

 где m1 - масса отрезка стержня, L0 , L1 - длины частей стержня.
где m1 - масса отрезка стержня, L0 , L1 - длины частей стержня. где m - модуль зацепления, z1 и z2 -число зубьев соответственно шестерни и колеса, а - угол профиля зубца рейки, а1 -угол зацепления.
где m - модуль зацепления, z1 и z2 -число зубьев соответственно шестерни и колеса, а - угол профиля зубца рейки, а1 -угол зацепления. где g -заряд конденсатора, W -энергия, накопленная в конденсаторе.
где g -заряд конденсатора, W -энергия, накопленная в конденсаторе. , где
, где 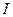 -сила тока, ρ; - удельное сопротивление материала, L - длина провода, r0 - радиус провода.
-сила тока, ρ; - удельное сопротивление материала, L - длина провода, r0 - радиус провода. , где u - деформация бруса, t - напряжение твердого тела.
, где u - деформация бруса, t - напряжение твердого тела. , где m - масса шара, r - радиус шара.
, где m - масса шара, r - радиус шара. где Pc - потери мощности на трение, r1 - коэффициент заполнения привода, r2 -коэффициент, учитывающий условие пуска двигателя, Pn - мощность, затрачиваемая на перемешивание, η - КПД привода.
где Pc - потери мощности на трение, r1 - коэффициент заполнения привода, r2 -коэффициент, учитывающий условие пуска двигателя, Pn - мощность, затрачиваемая на перемешивание, η - КПД привода.


