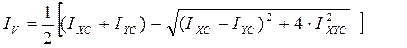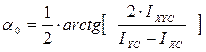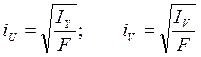Обработка элементов в одномерных массивах
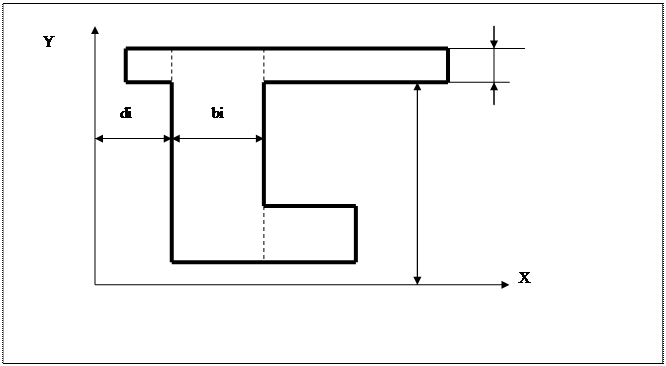
Для предложенной задачи составить графическую схему алгоритма и написать программу. Исходные данные для расчетов подобрать самостоятельно. Дана фигура (рисунок 2), которая может быть разбита на
Рисунок 2 - Заданное сечение
Оси X и Y проводятся так, чтобы они были параллельны сторонам рассматриваемого сечения. Расстояния от осей X и Y до ближайших сторон прямоугольников обозначаются соответственно Si и di. Координаты центра тяжести сложной фигуры определяются по формулам:
где Sx и Sy- статические моменты фигуры; F- площадь фигуры; Fi- площади отдельных простых частей; Xi и Yi- координаты центров тяжести этих частей
Моменты инерции сечения относительно осей X и Y определяются как сумма моментов инерции отдельных прямоугольников. При этом можно воспользоваться формулами преобразования при параллельном переносе осей:
Зная значения IX, IY, IXY, можно определить центральные моменты инерции:
Главные моменты инерции (
Вариант 1. Определить координаты центра тяжести YC сложной фигуры, состоящей из n участков. Вариант 2. Определить момент инерции IX сечения сложной фигуры относительно оси X. Вариант 3. Определить центральный момент инерции IXC сложной фигуры. Вариант 4. Определить координату XC центра тяжести сложной фигуры, состоящей из n участков.
Вариант 5. Определить главный момент инерции IV сложной фигуры, разбитой на отдельные простые части. Вариант 6. Определить центральный момент инерции IYC сложной фигуры. Вариант 7. Определить угол наклона оси U к оси XC – α0. Вариант 8. Определить координату центра тяжести XC сложной фигуры. Вариант 9. Определить главный момент инерции IU сложной фигуры, разбитой на отдельные простые части. Вариант 10. Определить момент инерции IY сечения сложной фигуры относительно оси Y. Вариант 11. Определить радиус инерции iU сложной фигуры. Вариант 12. Определить центральный момент инерции IXYC сложной фигуры. Вариант 13. Определить момент инерции IXY сложной фигуры. Вариант 14. Определить радиус инерции iV сложной фигуры. Вариант 15. Определить координаты центра тяжести YC и XC сложной фигуры, состоящей из n участков.
|
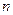прямоугольников высотой 
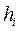и шириной 
.
;
.
;
.
, 
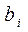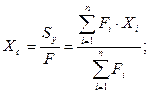
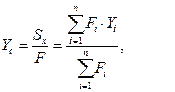
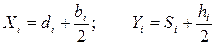
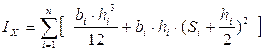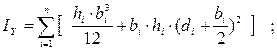
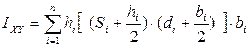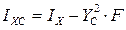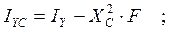
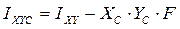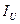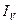), угол наклона 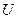оси 
к оси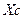 
(
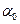) и радиусы инерции (
, 
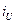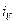) определяются соответственно по формулам:
; 
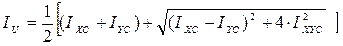