Линейные алгоритмы со взаимосвязанными вычислениями
Для каждой из нижеприведенных задач составить графическую схему алгоритма и написать программу.
Вариант 1. Определить предельную частоту вращения стержня
где ΔL – удлинение всего стержня,
где E – модуль упругости, E=2∙102 МПа, L-длина стержня, L=0,31 м, ρ; –плотность материала, ρ;=4800 кг/м3, ω=πn/30- угловая скорость вращения, n=160 об/мин, R=0,7 м. Определить силу инерции, действующую на стержень
где Z – расстояние от начала координат, Z=0,5м; F- площадь поперечного сечения стержня, F=10-4 м2. Вариант 2. Определить аналоги угловой скорости и ускорение шатуна:
где φ1 –угол наклона шатуна, φ1=0,98, а1, а2, а3-длины звеньев, а1=0,986, а2=2,39, а3=0,424. Вариант 3. Определить поправочную функцию сосуда и критическое напряжение
где
где K1C =74 МПа – коэффициент интенсивности напряжения, l =3∙10-3 м – глубина трещины, H =8,5∙10-3 м- толщина стенки сосуда, a =4,5∙10-3 м – протяженность трещины. Вариант 4. Определить угол наклона главной оси поперечного сечения бруса
Определить радиус инерции
где F0 – общая площадь сечения, F0=92,1,
Вариант 5. В кривошипно-ползунном механизме определить аналог угловой скорости ползуна
где i21- аналог угловой скорости шатуна,
φ2 – угол наклона шатуна,
φ1=1,023, а1, а2, а3 - параметры механизма, а1=1,33, а2=3,786, а3=0,87. Вариант 6. Определить наибольший изгибающий момент балки от динамичной нагрузки
где k = 0,5; l = 2,8; P0 = 10 кН,
где
E =2∙1011 – модуль упругости, IX =1290 см4, m =1500 кг, n =480 мин-1. Вариант 7. Определить коэффициент динамичности балки под действием нагрузки
где где r – коэффициент расчетной схемы,
b =0,3м, l =1,05 м – размеры балки, P =60 H, E =200 Гпа, h =0,4∙l – высота падения груза, r =0,98. Вариант 8. Определить параметры фрикционного сцепления: Z – число пар трения и Q – требуемая сила нажатия по формулам
где
μ; =0,15 – коэффициент трения, ρ; =196000 – допускаемое давление,
β; =2,5, Ne =159 кВт – мощность двигателя, ω; =330 с-1 – частота вращения коленвала, Rн =0,3 м, Rв =0,2 м – наружный и внутренний радиусы. Вариант 9. В кривошипно-шатунном механизме определить аналог скорости точки N по формулам
где
φ1=0,293, а1, а2, а3, а4 - параметры механизма, а1=2,31, а2=6,236, а3=1,08, а4=0,4, β=1,89. Вариант 10. Определить в статической системе перемещение сечения
где F2= F3=2∙F, F=20∙10-4 м2, E=200 ГПа, L2=3·a, L3=2·a, a=0,1 м. P1=P, P2=3∙P, P=0,127 МН. Определить энергию деформации
Вариант 11. Определить общий коэффициент запаса вала по формуле
τ-1=240, τа=30, φτ=0,7, τm=2, nσ=1,42 – коэффициент чувствительности материала. Вариант 12. Определить прочностную характеристику балки
где F - площадь сечения балки, F=F1-F2+F3, F1 =12a2, F2 =3a2, F3 =4a2, a =0,13 м, P – допускаемая сила по условию прочности, P=1,159 МН, yp =0,846∙a, xp =-a, xт =2∙a, yт =2,154∙a,
Определить прочностную характеристику сжатия балки
где ys =2,846∙a, xs = -a. Вариант 13. Для цилиндрической оболочки, находящейся под внутренним давлением определить радиальное перемещение W и изгибающий момент Mk
где
E=200000 МПа – модуль упругости, h=0,005 м – толщина оболочки, R=0,5 м – радиус срединной поверхности, P=50 МПа – давление, z=1,5. Вариант 14 Определить гибкость стержня круглого сечения по формуле:
где P =800 кН, δ; =160 МПа, φ; =0,6 – коэффициент снижения напряжения,
Вариант 15. Определить коэффициент запаса усталостной прочности
где φσ =0,12 – коэффициент чувствительности, КσD =2,0 – коэффициент при расчете амплитуды цикла, δ-1 =170 МПа,
Mmaxcm=1,03∙10-2 МН∙м – наибольший изгибающий момент от статической нагрузки, Mmaxдин=1,05∙10-2 МН∙м – наибольший изгибающий момент от динамической нагрузки, Wx =143 см3.
|

 ,
, ,
,
 ,
,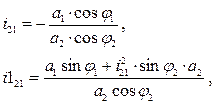
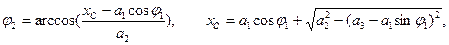
 для запаса прочности
для запаса прочности
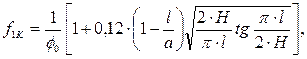
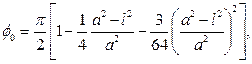

 , где
, где  - минимальный центральный момент,
- минимальный центральный момент, .
. ,
, =1820,
=1820,  =3116,
=3116,  =3856.
=3856.



 - коэффициент нарастания амплитуды колебаний,
- коэффициент нарастания амплитуды колебаний, - угловая частота двигателя, n – частота вращения ротора,
- угловая частота двигателя, n – частота вращения ротора, – угловая частота свободных колебаний,
– угловая частота свободных колебаний,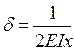 - прогиб в сечении,
- прогиб в сечении,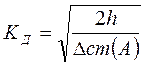 ,
, - статический прогиб в точке А,
- статический прогиб в точке А,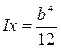 – осевой момент инерции,
– осевой момент инерции,
 - средний радиус трения,
- средний радиус трения, – максимальный момент в сцеплении,
– максимальный момент в сцеплении,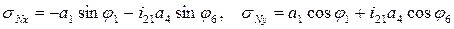 ,
, - угол наклона шатуна,
- угол наклона шатуна, - аналог угловой скорости шатуна,
- аналог угловой скорости шатуна, ,
, под действием реакции
под действием реакции 
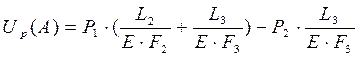 ,
,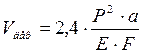
 , где
, где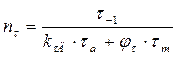 - частный коэффициент запаса,
- частный коэффициент запаса,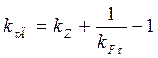 - расчетная амплитуда цикла,
- расчетная амплитуда цикла,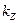 = 1,725,
= 1,725,  0,931- коэффициент влияния шероховатости поверхности,
0,931- коэффициент влияния шероховатости поверхности, ,
, - моменты инерции относительно осей x и y.
- моменты инерции относительно осей x и y.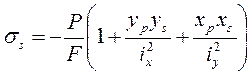 ,
, ,
, ,
, =0,3 – коэффициент Пуассона,
=0,3 – коэффициент Пуассона, ,
, - площадь в приближении,
- площадь в приближении,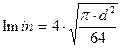 , μ = 0,7, l = 3 м, d = 9,6∙10-2 м.
, μ = 0,7, l = 3 м, d = 9,6∙10-2 м. ,
, - статическое напряжение,
- статическое напряжение, - динамическое напряжение,
- динамическое напряжение,


