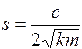Задача 1. Для динамической колебательной системы, содержащей массу, пружину и демпфер, вычислить множество значений функции амплитудно-частотной характеристики системы
Для динамической колебательной системы, содержащей массу, пружину и демпфер, вычислить множество значений функции амплитудно-частотной характеристики системы H(t) по формуле:
где коэффициент затухания системы s вычисляется по формуле:
Собственная частота незатухающих колебаний системы рассчитывается по формуле:
Резонансная частота системы (частота, на которой функция амплитудно-частотной характеристики достигает максимума) вычисляется по формуле:
В задаче используются следующие обозначения: m – масса системы; k – коэффициент жесткости пружины; с – коэффициент демпфирования демпфера; f – текущее значение частоты. При вычислении значений функции амплитудно-частотной характеристики в зависимости от частоты границы изменения частоты f и шаг ее изменения выбрать самостоятельно в области резонансной частоты колебательной системы. Исходные данные выбираются согласно таблице 3.1.
Таблица 3.1 – Исходные данные задачи 1
|

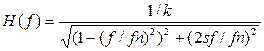 ,
,