Алгоритм входа-выхода
Метод входа выхода был разработан Фиенапом применительно к проблеме восстановления фазы по измерению одной интенсивности в области пространственного спектра. Функция комплексной амплитуды
где f – фокусное расстояние тонкой линзы, формирующей Фурье-спектр. Переход от преобразования Френеля (2.1) к преобразованию Фурье (2.9) означает, что в последнем случае следует использовать комбинацию ДОЭ плюс линза. Итеративное решение задачи восстановления фазы светового поля при помощи алгоритма входа-выхода имеет вид
где β - некоторый параметр
ɣ - область нарушения ограничений, накладываемых на заданную функцию поля,
- выходная функция,
Для решения проблемы синтеза ДОЭ предлагается выбирать приращение функции – в алгоритме входа-выхода в следующем виде:
где Другой инвариант итеративного алгоритма входа выхода для синтеза ДОЭ – маятниковый алгоритм. Предполагается, что фаза независима от модуля комплексной амплитуды света
*оптимальный выбор модуля и фазы на (n+1)-м шаге итерации принимает вид
|

 в области ДОЭ и
в области ДОЭ и  в плоскости Фурье (задней фокальной плоскости сферической линзы), в которой формируется изображение, связаны между собой при помощи двумерного преобразования Фурье:
в плоскости Фурье (задней фокальной плоскости сферической линзы), в которой формируется изображение, связаны между собой при помощи двумерного преобразования Фурье: , (2.9)
, (2.9) , (2.10)
, (2.10) ,
, (2.11)
(2.11)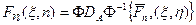 (2.12)
(2.12)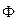 и
и  - прямое и обратное преобразование Фурье,
- прямое и обратное преобразование Фурье, - ограничивающий оператор в области ДОЭ:
- ограничивающий оператор в области ДОЭ: . (2.13)
. (2.13) , (2.14)
, (2.14) - заданное распределение интенсивностей в Фурье-плоскости,
- заданное распределение интенсивностей в Фурье-плоскости,  и
и  - входная и выходная функции или функции комплексной амплитуды в плоскости Фурье-изображения после и до выполнения ограничений.
- входная и выходная функции или функции комплексной амплитуды в плоскости Фурье-изображения после и до выполнения ограничений. , (2.15)
, (2.15)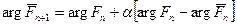 .
. .
.


