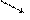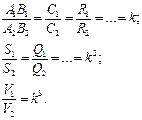ПИРАМИДА
«Многогранники»
Завдання І-го рівня 1. Обчислити об’єм піраміди, основою якої є прямокутник зі сторонами
2. Сторона основи правильної трикутної призми дорівнює ребро - 3. Обчислити площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 4. Обчислити площу бічної поверхні правильної шестикутної піраміди, сторона основи якої дорівнює 5. Ребро куба збільшили у 2 рази. У скільки разів збільшився об’єм куба? 6. Обчислити об’єм піраміди, основою якої є паралелограм зі сторонами
7. Обчислити площу бічної поверхні прямої призми, основа якої трикутник зі сторонами
8. Обчислити об’єм правильної трикутної призми, сторона основи якої дорівнює бічне ребро -
Завдання ІІ-го рівня 9. Основа прямої призми – ромб з діагоналями 10см і 24см. Менша діагональ призми дорівнює 26см. Обчисліть площу бічної поверхні призми. 10. Сторони основи прямого паралелепіпеда дорівнюють Менша діагональ утворює кут 11. Сторона основи правильної трикутної піраміди дорівнює площини основи під кутом 12. Бічна грань правильної чотирикутної піраміди нахилена до площини основи під кутом Відрізок, який сполучає середину висоти піраміди і середину апофеми, дорівнює Знайдіть об’єм піраміди. 13. Сторони перпендикулярного перерізу, який перетинає всі ребра нахиленого паралелепіпеда, дорівнюють якщо його бічне ребро дорівнює 14. Основа піраміди - трикутник зі сторонами який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2, рахуючи від вершин піраміди. Завдання ІІІ-го рівня 15. Основа піраміди - рівнобедрений трикутник з бічною стороною Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 16. Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної призми проведено переріз під кутом площа перерізу дорівнює
ПРИЗМА 1. прямая – бок. ребра 2. правил. – 1) прямая 2) в осн. прав. многоуг. 3. парал-д – в осн. парал-м (все грани парал-мы) 4. свойства: 1)против.грани = и ║ 2) диагонали ∩ в одной т. и т.∩ делятся пополам 5. прямой парал-д – в осн. парал-м бок. грани прямоугольники 6. прямоуг.пар-д – все грани прям-ки 7. свойства: 3) d2 = а2 + b2 + с2 8. куб – все грани квадраты
d c
a
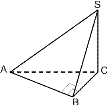
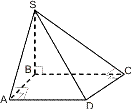
S
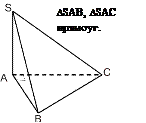
SА1В1С1 ~ SА2В2С2 А1 O1
В1
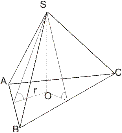
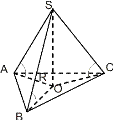
ПИРАМИДА 1. правил. – 1) в осн. прав. многоуг. 2) основание выс. в ц. многоуг. 2. тетраэдр – треуг. пирамида 3. правил. тетр. – все ребра =
1. ГДЕ РАСПОЛ. ОСН. ВЫСОТЫ?
ц. впис ц. опис. в верш. др. многоуг. 2. КАКОЙ МНОГОУГ. В ОСНОВАНИИ? S
B ПОДОБИЕ Все прав. многог-ки и шары подобны.
|

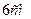 і
і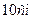 , а висота піраміди дорівнює
, а висота піраміди дорівнює 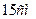 .
.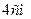 , а її бічне
, а її бічне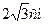 . Обчислити об’єм призми.
. Обчислити об’єм призми.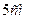 і
і 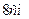 .
.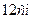 .
.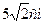 та кутом
та кутом 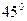 між ними, а висота піраміди дорівнює
між ними, а висота піраміди дорівнює 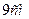 .
.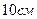 ,
, 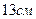 , а бічне ребро дорівнює
, а бічне ребро дорівнює 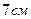 і
і 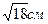 , кут між ними
, кут між ними 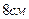 , а бічна грань нахилена до
, а бічна грань нахилена до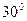 . Знайдіть площу повної поверхні піраміди.
. Знайдіть площу повної поверхні піраміди.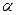 .
.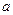 .
.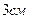 і
і 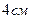 та складають між собою кут
та складають між собою кут 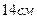 і
і 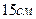 . Знайдіть площу перерізу,
. Знайдіть площу перерізу,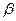 . Знайти об’єм піраміди.
. Знайти об’єм піраміди.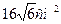 .
. основанию
основанию








 B1
B1 


 А С
А С b B
b B



 УСЕЧЕННАЯ ПИРАМИДА A2
УСЕЧЕННАЯ ПИРАМИДА A2




 (А2В2С2)║ (А1В1С1) B2 А1В1С1А2В2С2 – усеч.пир.
(А2В2С2)║ (А1В1С1) B2 А1В1С1А2В2С2 – усеч.пир.
 МНОГОГРАННИКИ
МНОГОГРАННИКИ