Лабораторная работа №5. Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу: №
Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:
| №
| 
| 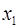
| 
| 
| 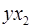
| 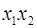
| 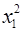
| 
| 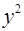
| |
|
|
|
|
|
|
|
|
|
| |
| 7,0
| 3,9
| 10,0
| 27,3
| 70,0
| 39,0
| 15,21
| 100,0
| 49,0
| |
| 7,0
| 3,9
| 14,0
| 27,3
| 98,0
| 54,6
| 15,21
| 196,0
| 49,0
| |
| 7,0
| 3,7
| 15,0
| 25,9
| 105,0
| 55,5
| 13,69
| 225,0
| 49,0
| |
| 7,0
| 4,0
| 16,0
| 28,0
| 112,0
| 64,0
| 16,0
| 256,0
| 49,0
| |
| 7,0
| 3,8
| 17,0
| 26,6
| 119,0
| 64,6
| 14,44
| 289,0
| 49,0
| |
| 7,0
| 4,8
| 19,0
| 33,6
| 133,0
| 91,2
| 23,04
| 361,0
| 49,0
| |
| 8,0
| 5,4
| 19,0
| 43,2
| 152,0
| 102,6
| 29,16
| 361,0
| 64,0
| |
| 8,0
| 4,4
| 20,0
| 35,2
| 160,0
| 88,0
| 19,36
| 400,0
| 64,0
| |
| 8,0
| 5,3
| 20,0
| 42,4
| 160,0
| 106,0
| 28,09
| 400,0
| 64,0
| |
| 10,0
| 6,8
| 20,0
| 68,0
| 200,0
| 136,0
| 46,24
| 400,0
| 100,0
| |
| 9,0
| 6,0
| 21,0
| 54,0
| 189,0
| 126,0
| 36,0
| 441,0
| 81,0
| |
| 11,0
| 6,4
| 22,0
| 70,4
| 242,0
| 140,8
| 40,96
| 484,0
| 121,0
| |
| 9,0
| 6,8
| 22,0
| 61,2
| 198,0
| 149,6
| 46,24
| 484,0
| 81,0
| |
| 11,0
| 7,2
| 25,0
| 79,2
| 275,0
| 180,0
| 51,84
| 625,0
| 121,0
| |
| 12,0
| 8,0
| 28,0
| 96,0
| 336,0
| 224,0
| 64,0
| 784,0
| 144,0
| |
| 12,0
| 8,2
| 29,0
| 98,4
| 348,0
| 237,8
| 67,24
| 841,0
| 144,0
| |
| 12,0
| 8,1
| 30,0
| 97,2
| 360,0
| 243,0
| 65,61
| 900,0
| 144,0
| |
| 12,0
| 8,5
| 31,0
| 102,0
| 372,0
| 263,5
| 72,25
| 961,0
| 144,0
| |
| 14,0
| 9,6
| 32,0
| 134,4
| 448,0
| 307,2
| 92,16
| 1024,0
| 196,0
| |
| 14,0
| 9,0
| 36,0
| 126,0
| 504,0
| 324,0
| 81,0
| 1296,0
| 196,0
| | Сумма
|
| 123,8
|
| 1276,3
|
| 2997,4
| 837,74
| 10828,0
| 1958,0
| | Ср. знач.
| 9,6
| 6,19
| 22,3
| 63,815
| 229,05
| 149,87
| 41,887
| 541,4
| 97,9
| Найдем средние квадратические отклонения признаков:
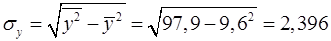 ; ;
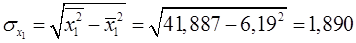 ; ;
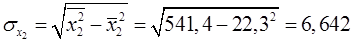 . .
Вычисление параметров линейного уравнения множественной регрессии.
Для нахождения параметров линейного уравнения множественной регрессии
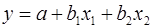
необходимо решить следующую систему линейных уравнений относительно неизвестных параметров 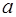 , ,  , , 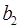 : :
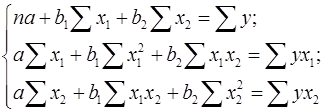
либо воспользоваться готовыми формулами:
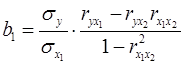 ; ;  ; ;
 . .
Рассчитаем сначала парные коэффициенты корреляции:
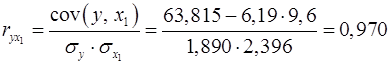 ; ;
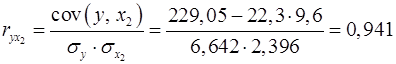 ; ;
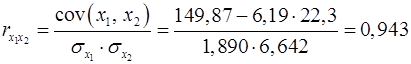 . .
Находим
 ; ;
 ; ;
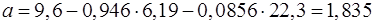 . .
Таким образом, получили следующее уравнение множественной регрессии:
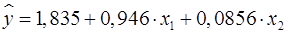 . .
Коэффициенты 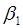 и и 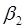 стандартизованного уравнения регрессии стандартизованного уравнения регрессии 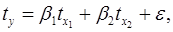 находятся по формулам: находятся по формулам:
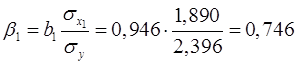 ; ;
 . .
Т.е. уравнение будет выглядеть следующим образом:
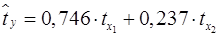 . .
Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации.
Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:
 . .
Вычисляем:
 ; ; 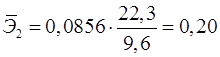 . .
Т.е. увеличение только основных фондов (от своего среднего значения) или только удельного веса рабочих высокой квалификации на 1% увеличивает в среднем выработку продукции на 0,61% или 0,20% соответственно. Таким образом, подтверждается большее влияние на результат  фактора фактора 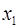 , чем фактора , чем фактора  . .
Коэффициенты парной корреляции мы уже нашли:
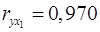 ; ;  ; ; 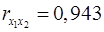 . .
Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость (факторы 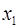 и и  явно коллинеарны, т.к. явно коллинеарны, т.к.  ). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения. ). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.
При двух факторах частные коэффициенты корреляции рассчитываются следующим образом:
 ; ;
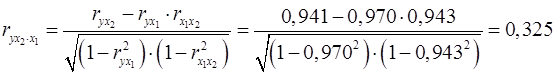 . .
Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.
Коэффициент множественной корреляции определить через матрицу парных коэффициентов корреляции:
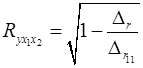 , ,
где
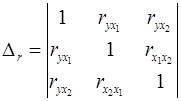
– определитель матрицы парных коэффициентов корреляции;
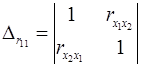
– определитель матрицы межфакторной корреляции.
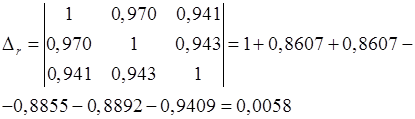 ; ;
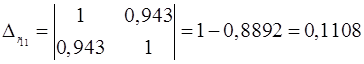 . .
Коэффициент множественной корреляции
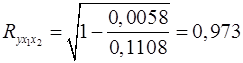 . .
Аналогичный результат получим при использовании других формул:
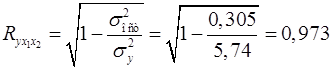 ; ;
 ; ;
 . .
Коэффициент множественной корреляции показывает на весьма сильную связь всего набора факторов с результатом.
Нескорректированный коэффициент множественной детерминации 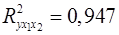 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 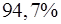 и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом. и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.
Скорректированный коэффициент множественной детерминации
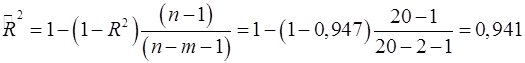
определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более  ) детерминированность результата ) детерминированность результата  в модели факторами в модели факторами 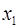 и и  . .
Оценку надежности уравнения регрессии в целом и показателя тесноты связи 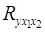 дает дает  -критерий Фишера: -критерий Фишера:
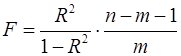 . .
В нашем случае фактическое значение  -критерия Фишера: -критерия Фишера:
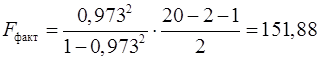 . .
Получили, что 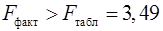 (при (при 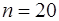 ), т.е. вероятность случайно получить такое значение ), т.е. вероятность случайно получить такое значение  -критерия не превышает допустимый уровень значимости -критерия не превышает допустимый уровень значимости 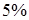 . Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи . Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи  . .
С помощью частных  -критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора -критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора 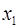 после после  и фактора и фактора  после после 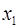 при помощи формул: при помощи формул:
 ; ;
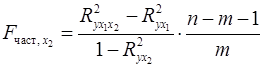 . .
Найдем 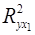 и и 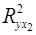 . .
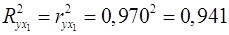 ; ;
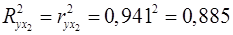 . .
Имеем
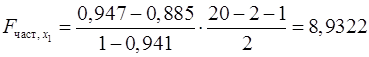 ; ;
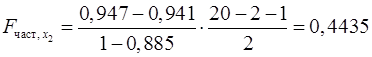 . .
Получили, что 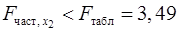 . Следовательно, включение в модель фактора . Следовательно, включение в модель фактора  после того, как в модель включен фактор после того, как в модель включен фактор 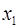 статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака  оказывается незначительным, несущественным; фактор оказывается незначительным, несущественным; фактор  включать в уравнение после фактора включать в уравнение после фактора 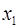 не следует. не следует.
Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения 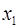 после после  , то результат расчета частного , то результат расчета частного  -критерия для -критерия для 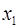 будет иным. будет иным. 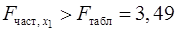 , т.е. вероятность его случайного формирования меньше принятого стандарта , т.е. вероятность его случайного формирования меньше принятого стандарта 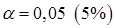 . Следовательно, значение частного . Следовательно, значение частного  -критерия для дополнительно включенного фактора -критерия для дополнительно включенного фактора 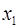 не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора 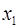 является существенным. Фактор является существенным. Фактор 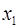 должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора  . .
Общий вывод состоит в том, что множественная модель с факторами 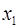 и и  с с 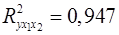 содержит неинформативный фактор содержит неинформативный фактор  . Если исключить фактор . Если исключить фактор  , то можно ограничиться уравнением парной регрессии: , то можно ограничиться уравнением парной регрессии:
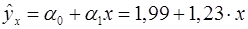 , , 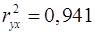 . .
Задание для самостоятельной работы (выполнить по аналогии с примером)
По  предприятиям региона изучается зависимость выработки продукции на одного работника предприятиям региона изучается зависимость выработки продукции на одного работника  (тыс. руб.) от ввода в действие новых основных фондов (тыс. руб.) от ввода в действие новых основных фондов 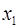 ( (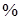 от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих  ( (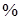 ). ).
| Номер предприятия
| 
| 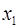
| 
| Номер предприятия
| 
| 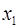
| 
| |
|
| 3,6
|
|
|
| 6,3
|
| |
|
| 3,6
|
|
|
| 6,4
|
| |
|
| 3,9
|
|
|
|
|
| |
|
| 4,1
|
|
|
| 7,5
|
| |
|
| 3,9
|
|
|
| 7,9
|
| |
|
| 4,5
|
|
|
| 8,2
|
| |
|
| 5,3
|
|
|
|
|
| |
|
| 5,3
|
|
|
| 8,6
|
| |
|
| 5,6
|
|
|
| 9,5
|
| |
|
| 6,8
|
|
|
|
|
| Требуется:
Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
С помощью  -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации 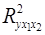 . .
С помощью частных  -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора 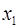 после после  и фактора и фактора  после после 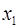 . .
Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Лабораторная работа №5
«Введение в множественную регрессию»
Часто приходится использовать несколько независимых переменных (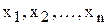 ) для предсказания значения зависимой переменной. В этих случаях для оценки интересующей нас зависимости можно применять либо вариант множественной регрессии в Пакете анализа, либо функцию ЛИНЕЙН(). ) для предсказания значения зависимой переменной. В этих случаях для оценки интересующей нас зависимости можно применять либо вариант множественной регрессии в Пакете анализа, либо функцию ЛИНЕЙН().
Множественная регрессия предполагает, что зависимость между y и 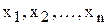 описывается уравнением вида описывается уравнением вида
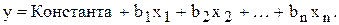
Программа Excel вычисляет значения Константы и 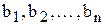 для расчёта с помощью данного уравнения как можно более точных (с точки зрения минимизации суммы квадратов ошибок) прогнозируемых значений. для расчёта с помощью данного уравнения как можно более точных (с точки зрения минимизации суммы квадратов ошибок) прогнозируемых значений.

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
САНИТАРНО-МИКРОБИОЛОГИЧЕСКОЕ ИССЛЕДОВАНИЕ ВОДЫ, ВОЗДУХА И ПОЧВЫ Цель занятия.Ознакомить студентов с основными методами и показателями...
Меры безопасности при обращении с оружием и боеприпасами 64. Получение (сдача) оружия и боеприпасов для проведения стрельб осуществляется в установленном порядке[1].
65. Безопасность при проведении стрельб обеспечивается...
|
КОНСТРУКЦИЯ КОЛЕСНОЙ ПАРЫ ВАГОНА Тип колёсной пары определяется типом оси и диаметром колес. Согласно ГОСТ 4835-2006* устанавливаются типы колесных пар для грузовых вагонов с осями РУ1Ш и РВ2Ш и колесами диаметром по кругу катания 957 мм. Номинальный диаметр колеса – 950 мм...
Философские школы эпохи эллинизма (неоплатонизм, эпикуреизм, стоицизм, скептицизм). Эпоха эллинизма со времени походов Александра Македонского, в результате которых была образована гигантская империя от Индии на востоке до Греции и Македонии на западе...
Демографияда "Демографиялық жарылыс" дегеніміз не? Демография (грекше демос — халық) — халықтың құрылымын...
|
|


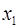


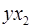
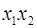
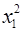

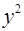
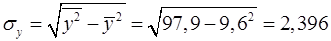 ;
;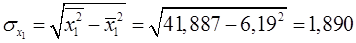 ;
;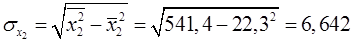 .
.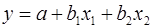
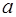 ,
,  ,
, 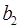 :
: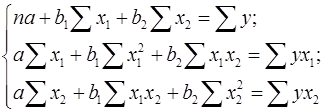
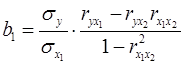 ;
;  ;
; .
.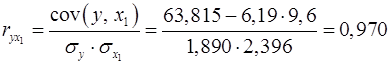 ;
;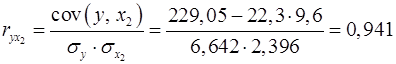 ;
;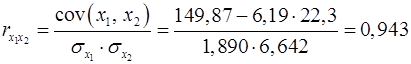 .
. ;
; ;
;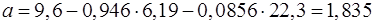 .
.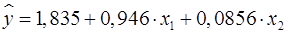 .
.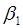 и
и 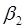 стандартизованного уравнения регрессии
стандартизованного уравнения регрессии 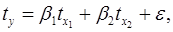 находятся по формулам:
находятся по формулам: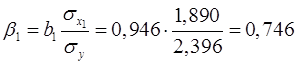 ;
; .
.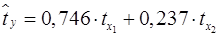 .
. .
. ;
; 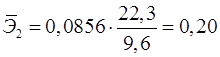 .
.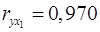 ;
;  ;
; 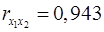 .
. ). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.
). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения. ;
;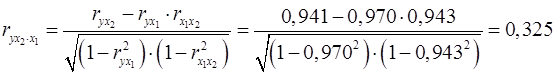 .
.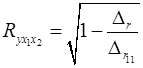 ,
,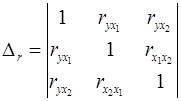
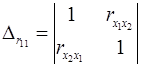
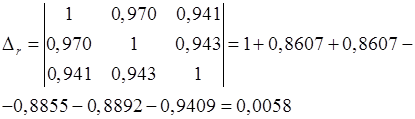 ;
;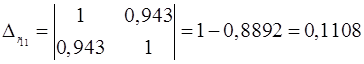 .
.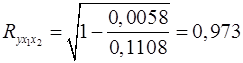 .
.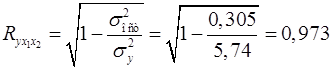 ;
; ;
; .
.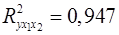 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет
оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 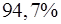 и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.
и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.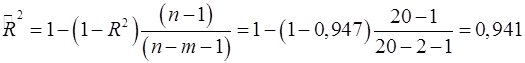
 ) детерминированность результата
) детерминированность результата 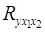 дает
дает  -критерий Фишера:
-критерий Фишера: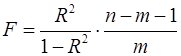 .
.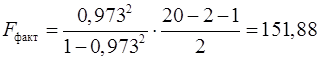 .
.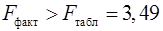 (при
(при 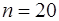 ), т.е. вероятность случайно получить такое значение
), т.е. вероятность случайно получить такое значение 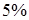 . Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи
. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи  .
. ;
;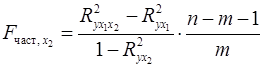 .
.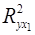 и
и 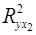 .
.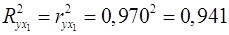 ;
;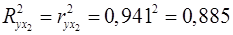 .
.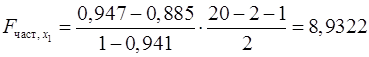 ;
;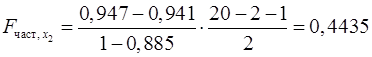 .
.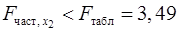 . Следовательно, включение в модель фактора
. Следовательно, включение в модель фактора 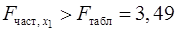 , т.е. вероятность его случайного формирования меньше принятого стандарта
, т.е. вероятность его случайного формирования меньше принятого стандарта 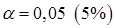 . Следовательно, значение частного
. Следовательно, значение частного 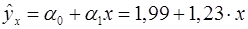 ,
, 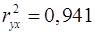 .
. предприятиям региона изучается зависимость выработки продукции на одного работника
предприятиям региона изучается зависимость выработки продукции на одного работника 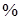 от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих
от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих 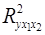 .
.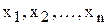 ) для предсказания значения зависимой переменной. В этих случаях для оценки интересующей нас зависимости можно применять либо вариант множественной регрессии в Пакете анализа, либо функцию ЛИНЕЙН().
) для предсказания значения зависимой переменной. В этих случаях для оценки интересующей нас зависимости можно применять либо вариант множественной регрессии в Пакете анализа, либо функцию ЛИНЕЙН().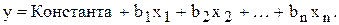
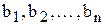 для расчёта с помощью данного уравнения как можно более точных (с точки зрения минимизации суммы квадратов ошибок) прогнозируемых значений.
для расчёта с помощью данного уравнения как можно более точных (с точки зрения минимизации суммы квадратов ошибок) прогнозируемых значений.


