ВВЕДЕНИЕ. Загружаем среду «Чертеж»Загружаем среду «Чертеж»
Нажимаем кнопку «Виды детали» и в появившемся окне указываем деталь или сборочную единицу. Нажимаем кнопку «Открыть»
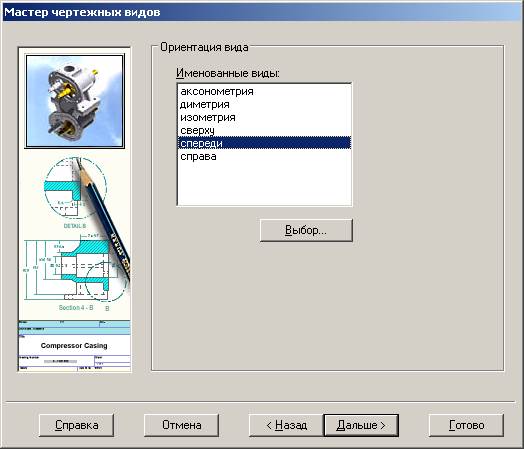
Переходим в окно «Мастер чертежных видов».
Далее убираем галочки. Нажимаем «Дальше»
Указываем на вид «Спереди» и кнопку «Выбор». Появляется окно главного вида.
Если главный вид нас не устраивает, то используя кнопку
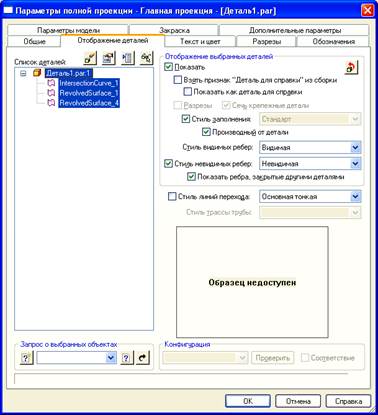
Указываем необходимые виды детали и нажимаем «Готово». Переходим в среду деталь. Указываем масштаб и нажимаем кнопку «параметры отображения детали»
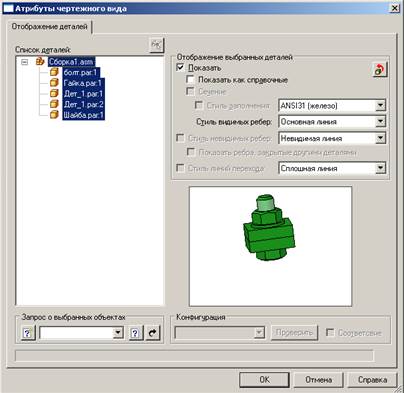
Устанавливаем необходимые стили и нажимаем кнопку «Ок». Размещаем видовой квадрат приблизительно в середине и нажимаем ЛКМ.
1. Установка атрибутов чертежного вида 2. Выберите элемент на чертежном виде. 3. Поместите курсор на рамку чертежного вида и щелкните ЛКМ. 4. В меню "Правка" выберите команду "Атрибуты". 5. В диалоговом окне атрибутов задайте требуемые параметры.
Нажмите кнопку «Ок». Далее проставляем необходимые размеры и оси симметрии. Далее заполняем основную надпись.
РАЗВЕРТКА ПОВЕРХНОСТИ. Разверткой называется плоская фигура, полученная совмещением поверхности тела с плоскостью.
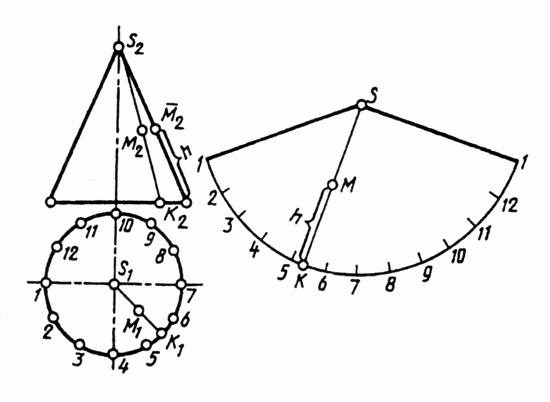
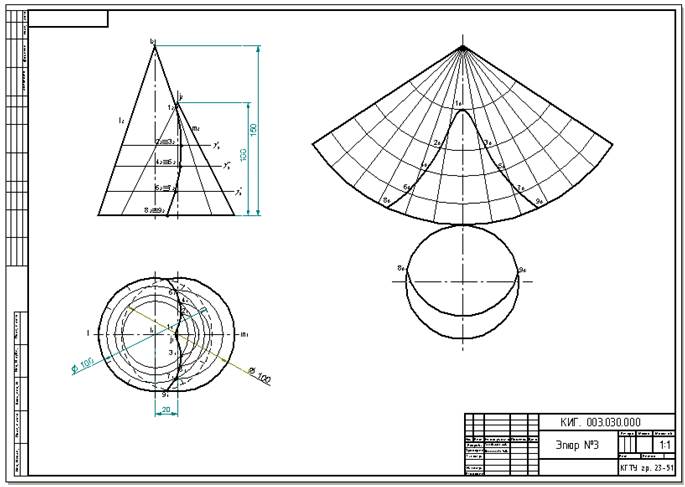
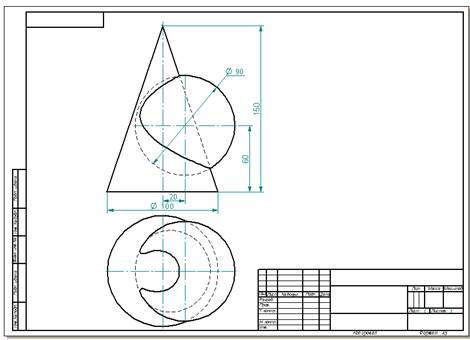
Развертка конусов производится по принципу развертывания пирамиды, для чего поверхность конуса предварительно аппроксимируют n - гранной пирамидой. На рис. выполнено построение развертки наклонного конуса. Основание конуса разделено на 8 частей. Натуральные величины образующих определены методом вращения.
Для построения ее используем то, что очерковая образующая конуса L на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку. Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим ее горизонтальную проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из проекции точки M2 проведем горизонтальную линию до пересечения с очерковой образующей L и получим точкуМ2. Расстояние от основания конуса до точки M2 по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.
Задание выполнено. ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ Программа AutoCAD — универсальная графическая система, используемая для построения любых изображений инженерного характера: машиностроительных, строительных, архитектурных, электротехнических и т.д. В то же время каждая из этих областей имеет свою специфику и ставит свои задачи. Неотъемлемой частью высшего технического образования является изучение курса начертательной геометрии и инженерной графики. Будущие инженеры независимо от избранной специальности изучают эти дисциплины. Программа обучения строится и воплощается в учебном процессе с учетом профиля будущей деятельности. Для специальностей ИСТ и ПОВТ целью изучения курса является формирование компьютерной грамотности, умение работать с различными графическими пакетами и использовать их в практической деятельности. Одним из таких пакетов является система AutoCAD. Согласно общеобразовательным стандартам проведение практических занятий предусмотрено на компьютере. Это налагает определенные требования на ведение учебного процесса. Освоение графической системы AutoCAD должно осуществляться параллельно с поисками решений задач по инженерной графике с применением знаний по геометрии, ЕСКД и возможностями САПРа. Заметим, что результат решения задачи может быть достигнут различными путями. Для будущих специалистов указанного профиля наиболее рациональным является использование возможностей графической системы, которая берет на себя рутинную работу по реализации решения задач. В основе этой системы запрограммированы теоретические положения начертательной и аналитической геометрии, методов вычислительной техники и т. д. В связи с целями изучения курса для указанных специальностей целесообразно выполнять графические работы (эпюры) средствами системы AutoCAD. Если студенты других специальностей выполняют их вручную, строя линии пересечения поверхностей способами посредников (секущих плоскостей, концентрических и эксцентрических сфер), то студенты этих специальностей идут от создания объема пересекающихся тел, их проецирования на координатные плоскости проекций, а поставленную задачу выполняет сама система, используя фактически метод начертательной геометрии (аппроксимацию), при котором кривая неразвертываемая поверхность заменяется развертываемой, Итоговое решение задачи сводится к построению линии пересечения плоских отсеков и это дает возможность системе по множеству точек построить любую линию пересечения поверхностей, с любой наперед заданной точностью. Кроме того, сформированную модель можно рассмотреть с различных точек зрения, поворачивая ее в виртуальном пространстве. Освоение одной из графических систем будущими специалистами, приобретение навыков работы с одной из них позволит им при необходимости изучить и другие системы и использовать умение работать с ними в различных областях. Например, участвовать в различных инженерных проектах, выполняя при этом свои функции, рекламно-оформительских работах, формировать поверхности для архитектурных сооружений и, проявляя творческую активность, искать применение полученных навыков для реализации своих идей. Следует отметить, что для выполнения работ по инженерной графике
|
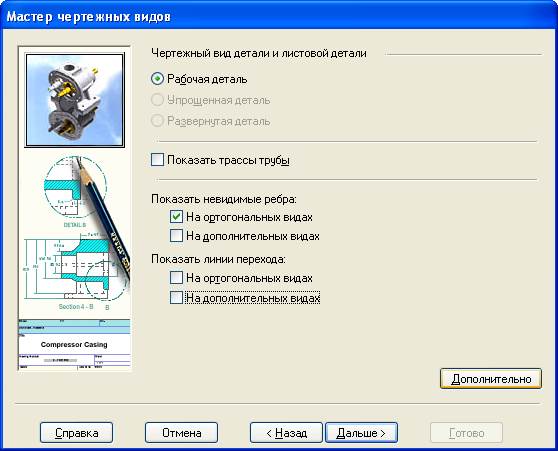
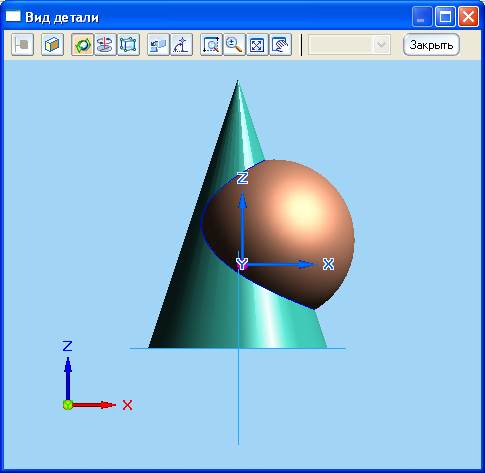
, поворачиваем в нужное положение и нажимаем «закрыть». Возвращаемся в окно «Мастер чертежных видов».
.
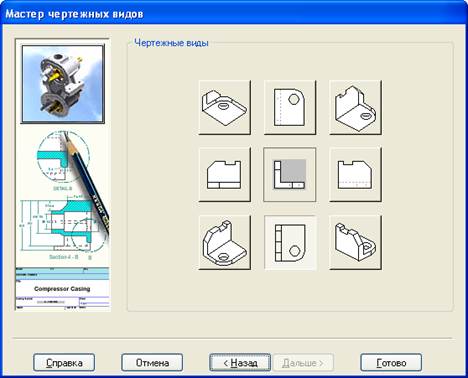
Для построения многогранной поверхности необходимо совместить с плоскостью все ее грани. Для построения развертки поверхности в общем случае надо в нее вписать многогранную поверхность и совместить с плоскостью. Поверхности, которые разворачиваются на плоскость без разрывов и складок, называются развертываемыми. К ним относятся линейчатые поверхности, у которых образующие параллельны или пересекаются (цилиндры, торсы, конусы). Остальные поверхности неразвертываемые. Развертки обладают многими одинаковыми свойствами самих поверхностей: равенством длинами прямых, равенством углов между линиями, параллельностью прямых. Развертки простых фигур можно строить и математически. Для цилиндра - это прямоугольник с длиной S = 2pR; для конуса - сектор с углом при вершине j= 2 pR / l (l - длина образующей). Однако чаще это сложные поверхности с вырезами и срезами на них, развертки которых возможно только использую графические приемы. Основной метод графического построения разверток - это аппроксимация заданной поверхности в виде многогранной поверхности. Часто вписывают многогранник с гранями в виде треугольников. Данный способ называется способом триангуляции. Самой трудоемкой частью при построении разверток является определение натуральной величины граней вписываемого в поверхность многогранника. Имеется ряд способов и приемов, сокращающих эту работу и облегчающих построение разверток. К ним относятся способ треугольников, способ нормального сечения и способ раскатки, которые, в свою очередь, используют, методы определения натуральной величины граней методами замены плоскостей проекций (ортогонального проецирования по нормали к плоскости грани) или вращения вокруг проецирующих осей.
