Свойства ПР
Непрерывные случайные величины (НСВ). Плотность распределения Определение. Случайная величина ξ с ФР F (x) называется НСВ, если существует функция Если ПР – непрерывная функция, то по теореме о производной от определенного интеграла по переменному верхнему пределу F’(x)=f(x) (см. свойство 4) ПР). Поэтому часто определение ПР случайной величины ξ с функцией распределения F(x) дают в виде f(x)=F’(x), если производная от функции распределения существует.
Свойства ПР
1)
Рисунок
2) Для ||
3) ||
Следствие. Как правило,
4) Если f (x) – непрерывна, то
Отсюда следует, что
5) График ПР наглядно представляет ξ (в какой интервал она попадает с какой вероятностью): для фиксированного Δ x
График
График ПР f (x) наглядно характеризует случайную величину ξ
Аналог (по свойствам) ПР в случае ДСВ – ее многоугольник распределения. На практике по результатам наблюдения случайной величины ξ часто оценивается ПР ξ, а затем ФР ξ! Замечание. В отличие от ФР F(x) (
|
наз. плотностью распределения (ПР) случайной величины ξ.
- геометрический смысл несобственного интеграла 
от неотрицательной функции f (x).
рисунок
- конечная площадь).
как производная неубывающей функции – ФР F(x).
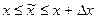
) плотность распределения f(x) может принимать значения, большие 1, но на интервалах малой длины, т.к. 
.
