Ковариация и коэффициент корреляции. Как оценить силу стохастической связи случайных величин X и Y ?
Как оценить силу стохастической связи случайных величин X и Y?
В общем случае (= MX + MY)
Поэтому, если X и Y зависимы, то
Зависимость X и Y можно оценить через свойства математического ожидания: X и Y – независимы =>
Заметим, что
Определение. Ковариация случайных величин X и Y - число
Коэффициент корреляции случайных величин X и Y - число
Для дискретных случайных величин (X, Y)
Свойства cov (X, Y) и r
1) X и Y – независимы => cov (X, Y) = 0 => r = 0. Обратное не верно! 2) 3) 4) r не меняется при линейных преобразованиях X и Y:
5) при r = -1 a < 0. Это – недостаток коэффициента корреляции r: r показывает, насколько стохастическая зависимость между X и Y близка к линейной (описывается линейной функциональной зависимостью). Поэтому из | r | << 1
Пример. Известно, что для некоторой возрастной категории людей связь веса человека (случайная величина X) и его роста (случайная величина Y) приближенно описывается функциональной зависимостью – уравнением линии регрессии y=x+110 (*). Возникает вопрос: «Насколько хорошо стохастическая зависимость случайной величины Y от случайной величины X характеризуется этой функциональной зависимостью для конкретной группы людей, например, для студентов данной группы?» Так как линия регрессии в данном примере является прямой, оценку доли функциональной зависимости (*) случайной величины Y от случайной величины X дает коэффициент корреляции r между случайными величинами X и Y, вычисленный для исследуемой группы студентов. Если полученное значение r коэффициента корреляции близко к единице, то формула (*) достаточно точно отражает стохастическую зависимость веса и роста студентов в этой группе.
Двумерное нормальное распределение случайных величин (X, Y) Для
где
В случае, когда X и Y - независимые нормально распределенные случайные величины с плотностями распределений
Аналитический вид плотности нормального распределения – см. в разделе «Нормальное распределение».
|

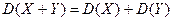 для независимых X и Y.
для независимых X и Y.


 Поэтому, если X и Y зависимы, то
Поэтому, если X и Y зависимы, то 


 (*)
(*)

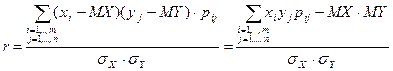
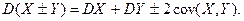



 связаны линейной зависимостью:
связаны линейной зависимостью:  при r =1 a > 0,
при r =1 a > 0, => либо функциональная зависимость Y от Х далека от линейной, либо стохастическая связь X и Y слабая. Из-за этого r применяют при линейной регрессии Y по Х или X по Y.
=> либо функциональная зависимость Y от Х далека от линейной, либо стохастическая связь X и Y слабая. Из-за этого r применяют при линейной регрессии Y по Х или X по Y. это распределение определяется совместной ПР
это распределение определяется совместной ПР , (*)
, (*) так как при r = ±1 X и Y линейно зависимы.
так как при r = ±1 X и Y линейно зависимы. и
и  соответственно, совместная плотность распределения X и Y равна произведению плотностей нормальных распределений
соответственно, совместная плотность распределения X и Y равна произведению плотностей нормальных распределений  и
и  :
: .
.


