Свойства. Следовательно, некоррелированные нормальные случайные величины независимы.
1) (!) При r = 0 Следовательно, некоррелированные нормальные случайные величины независимы. 2) Линии регрессии
3) Скедастические линии – прямые || Ox, Oy: (гомоскедаксичность)
Аналогично,
Корреляционные отношения
Корреляционные отношения характеризуют силу функциональной зависимости X и Y, когда линии регрессии – не прямые.
Определим В дискретном случае
В дискретном случае
Справедлива формула разложения дисперсии
определяется определяется случайными факторами, случайными факторами, действующими действующими на только на Y и не Y через Х. действующими на Х
Из (1) следует
Определение.
Свойства
1) 2) 3) (из дискретного случая: все слагаемые в сумме 4) r – коэффициент корреляции Х и Y
Точная связь r и η; - учебник Плехановки.
5) Если 6) Из 7) Связи между
|

 независимы.
независимы.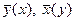 - прямые:
- прямые: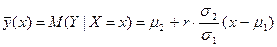 - прямая.
- прямая.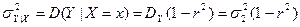 - остаточная, не коррелированная часть
- остаточная, не коррелированная часть  , определяемая случайными факторами, действующими на Y, но не действующая на Х.
, определяемая случайными факторами, действующими на Y, но не действующая на Х.
 и
и 
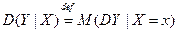 - средневзвешенное от условных дисперсий
- средневзвешенное от условных дисперсий 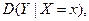 мера рассеяния Y вокруг
мера рассеяния Y вокруг 

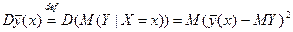 - мера рассеяния
- мера рассеяния  вокруг MY.
вокруг MY.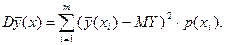
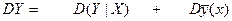 (1)
(1)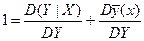 (2)
(2)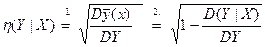
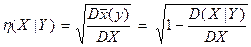
 (в (1) все слагаемые ≥ 0).
(в (1) все слагаемые ≥ 0).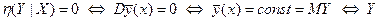 не коррелирует с Х, т.е. в стохастической зависимости Y от Х нет функциональной части. Но из
не коррелирует с Х, т.е. в стохастической зависимости Y от Х нет функциональной части. Но из  не следует независимость Х и Y.
не следует независимость Х и Y. нет рассеяния Y относительно
нет рассеяния Y относительно 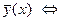
 неотрицательны =>
неотрицательны =>  ó
ó  стохастическая зависимость Y от Х полностью описывается функциональной зависимостью - функцией
стохастическая зависимость Y от Х полностью описывается функциональной зависимостью - функцией  , т.к. r учитывает силу только линейной зависимости Y от Х.
, т.к. r учитывает силу только линейной зависимости Y от Х.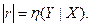
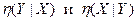 нет (возможно, одно из отношений равно 1, а другое - 0). Но, если
нет (возможно, одно из отношений равно 1, а другое - 0). Но, если  то Y - монотонная функция от Х.
то Y - монотонная функция от Х.


