СВЯЗИ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
Пусть X, Y - случайные величины на Ω. X, Y независимы
X, Y – функционально зависимы ó существует функция f: Y = f (X). X, Y – стохастически (вероятностно) зависимы ó X и Y не являются независимыми, но не являются и функционально зависимыми.
Как правило, стохастическая зависимость X и Y возникает, когда X и Y формируются под действием ряда случайных факторов, часть из которых действует одновременно на X и на Y. Например, пусть U, V, W - случайные факторы,
Как описать зависимость X и Y и её силу?
Корреляционная зависимость X и Y (та часть зависимости X и Y, которая описывается функционально). Описывается двумя линиями регрессии:
фиксированной Y = y.
Определение. Если Аналогично, В случае некоррелированных случайных величин X и Y их стохастическая зависимость (если она существует) не имеет функционального компонента.
График.
По теореме об устойчивости средних уравнение регрессии
Уравнения линий регрессии Для непрерывных X и Y так как
Для дискретных X и Y центр масс
Насколько точно это функциональной описание зависимости Y от Х соответствует реальной стохастической зависимости Y от Х показывают условные дисперсии:
Т.о.
Графики
Учебник Плехановки: Экстремальное свойство условного математического ожидания. M (Y | X) отражает (в среднем) зависимость Y от Х с минимальной среднеквадратичной погрешностью (т.е. с минимальной дисперсией!): для любой функции y = f (x)
Если
Точность описания функциональной зависимости X и Y линиями регрессии характеризуют скедастические линии – условные дисперсии
|

 - функция распределения случайной величины X,
- функция распределения случайной величины X,  - функция распределения случайной величины Y,
- функция распределения случайной величины Y, 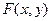 - совместная функция распределения случайной величины (X, Y).
- совместная функция распределения случайной величины (X, Y).
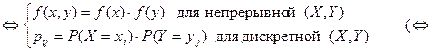 условные вероятности = безусловным вероятностям)
условные вероятности = безусловным вероятностям)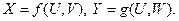 Тогда X и Y могут быть стохастически зависимы.
Тогда X и Y могут быть стохастически зависимы.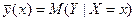 - условное математическое ожидание случайной величины Y при фиксированной X = x,
- условное математическое ожидание случайной величины Y при фиксированной X = x,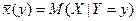 - условное математическое ожидание случайной величины X при
- условное математическое ожидание случайной величины X при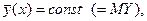 то случайная величина Y не коррелирует с X.
то случайная величина Y не коррелирует с X.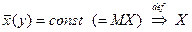 не коррелирует с Y. Тогда линии регрессии – прямые параллельные осям Ox или Oy.
не коррелирует с Y. Тогда линии регрессии – прямые параллельные осям Ox или Oy. дает наилучшее описа-ние функциональной зависимости Y от Х (см. ниже экстремальное свойство условного мате-матического ожидания из учебника Плехановки, с.258).
дает наилучшее описа-ние функциональной зависимости Y от Х (см. ниже экстремальное свойство условного мате-матического ожидания из учебника Плехановки, с.258).

 -
- расположенных на прямой
расположенных на прямой  в точках
в точках 

 - скедастические (изменчивые) линии.
- скедастические (изменчивые) линии. отражают точность описания зависимости Y от Х и X от Y с помощью регрессий
отражают точность описания зависимости Y от Х и X от Y с помощью регрессий 
 - СКО сл.в.
- СКО сл.в.  от
от 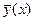 .
.
 т.е. не зависит от х, то Y не коррелирует с Х.
т.е. не зависит от х, то Y не коррелирует с Х.


