Міністерство аграрної політики України
1. Ліфт вагою Р = 6 000 Н піднімають вгору з постійним прискоренням а =1,4 м/сек2. Яка робота виконується, якщо ліфт піднімається на 10м?(6,86×104Дж) 2. Для тягових двигунів електропоїзда при русі з швидкістю u=54 км/год потрібна потужність N=900 кВт. Коефіцієнт корисної дії електричних двигунів і передавальних механізмів 3. Водій автомобіля, що рухається з швидкістю uраптом побачив перед собою на відстані s широку стіну. Що йому вигідніше: загальмувати, чи звернути вбік?(Вигідніше гальмувати ніж повертати.) 4.Поїзд вагою Р =6×106Н нерівномірно піднімається на гору. Підйом гори h =5 м на кілометр шляху. Сила тертя FT =104Н. Швидкість поїзда u =72 км/год. Визначити потужність тепловоза.(800кВт) 5.Тепловоз потужністю N =1800кВттягне поїзд масою т =2000т. Коефіцієнт опору k =0,005. Яка буде максимальна швидкість поїзда? З яким прискоренням рухається поїзд в моменти часу, коли його швидкість становить u1=4м/с і u2=12м/с? (u=18,3м/с, а 1=0,176м/с2, а 2=0,026м/с2). 6.Ліфт вагою Р =2×104 Н піднімають тросом, кожний метр якого важить 20Н, з шахти глибиною 200 м. Яка при цьому виконується робота? Знайти коефіцієнт корисної дії установки.(44×105Дж, 0,91) 7. n однорідних плит лежать горизонтально на поверхні землі одна біля одної. Кожна з плит важить Р і має товщину h. Яку найменшу (теоретично) роботу треба виконати, щоб скласти плити одна на одну у вигляді колони?( 8.Кусок льоду один раз кидають під кутом a=450 до горизонту, а другий раз пускають з такою ж швидкістю ковзати по льоду. Знайти коефіцієнт тертя, якщо в другому випадку кусок льоду перемістився на відстань, в 10 раз більшу, ніж в першому випадку.(0,05) 9.Ковзаняр, розігнавшись до швидкості u =27 км/год, хоче виїхати на крижану гору. На яку висоту від початкового рівня виїде ковзаняр з розгону, якщо підйом гори становить h=0,5м на кожні s =10м по горизонталі і коефіцієнт тертя ковзанів по льоду k = 0,02?(2м) 10. Ковзаняр, стоячи на ковзанах, кидає вперед в горизонтальному напрямі тягар вагою 100 Н з швидкістю 3 м/сек. Визначити коефіцієнт тертя ковзанів по льоду і виконану ковзанярем роботу, якщо його вага 600 Н і він відкотився після кидання на 0,5 м. (m=0,025, 53,6Дж) 11. Тіло масою т =500г, кинуте під кутом a=45° до горизонту, упало на горизонтальну поверхню на відстані s=16 м. Знайти роботу, затрачену на кидання тіла.(39,2Дж) 12. Тіло кинуте в горизонтальному напрямі з початковою швидкістю u=15 м/с. Через скільки секунд кінетична енергія тіла збільшиться вдвоє? Прийняти g =10 м/с?; опір повітря не враховувати.(1,5с) 13. Побудувати графіки залежності від часу кінетичної, потенціальної і повної енергії каменя масою 1 кг, кинутого вертикально вгору з швидкістю 9,8м/с. 14. Гвинтівка масою 3 кг підвішена горизонтально на двох паралельних нитках. При пострілі, в результаті віддачі, вона відхилилась вгору на 19,6 см. Маса кулі 10 г. Визначити швидкість, з якою вилетіла куля.(-588м/с) 15. Літак масою 1тлетить горизонтально на висоті 1200 м з швидкістю 50 м/с. При виключеному двигуні літак робить планеруючий політ і досягає Землі з швидкістю 25 м/с. Визначити силу опору повітря при спуску, приймаючи довжину спуску 8 км. (1587Н) 16. З артилерійської гармати масою 1000 кг вилітає в горизонтальному напрямі снаряд масою 10 кг. Яка частина роботи, виконаної пороховими газами, витрачається на віддачу?(1%) 17. Автомобілі з встановленими на них двигунами потужністю N1 i N2 розвивають швидкості u1 i u2 відповідно. З якою швидкістю їхатимуть автомобілі, якщо їх з'єднати тросом?( 18. Визначити кінетичну енергію тіла, кинутого в горизонтальному напрямі з висоти 100 м, в момент приземлення, якщо вага тіла 5Н і початкова швидкість 10 м/с. (525,5Дж) 19. Поїзд масою т =800твиїжджає з швидкістю u=30 м/с на прямолінійний відрізок шляху, нахилений до горизонту під кутом 20. Нехай тіло масою т знаходиться в поїзді, що рухається з швидкістю u. В такому разі воно має відносно землі кінетичну енергію 21. За допомогою копра забивають у грунт палю вагою Р =3×103 Н. При одному ударі молотом копра паля заглиблюється на 5 см. Визначити середню силу опору грунту, якщо молот вагою Р1=102 Н падає на палю з висоти Н=2м. Яка частина енергії падаючого молота використовується на роботу по подоланню сили опору грунту? Яка частина енергії йде на нагрівання і деформацію тіл? Вважати, що при падінні молота на нього діє середня сила опору повітря F= 0,1Р1. (13200Н, Е2/Е1=2,5) 22 Куля масою т =20 г ударяє з швидкістю u 0=400 м/с в дерев'яний брусок масою М =5 кг, підвішений на нитці довжиною l =4 м (балістичний маятник), і застряє в ньому. Визначити кут, на який відхилиться маятник.(a=15°) 23. Визначити коефіцієнт корисної дії транспортера, якщо за добу він переносить 2×107Н вантажу з рівня землі на висоту 5 м. Потужність двигуна 1,84 кВт. (0,63) 24. Тягар вагою Р= 103 Нприв'язаний до кінця вірьовки, намотаної на лебідку. Вантаж і лебідка знаходяться на деякій висоті. Тягар починає падати, причому вірьовка натягується, коли тягар пролетів h =12 м. Після цього починає з тертям розкручуватися лебідка. Яку мінімальну довжину вірьовки довелося витравити до повної зупинки тягаря, якщо міцність вірьовки (15м)? 25. Автомобіль масою т =103кгрухається з гори з уклоном 4 м на кожні 100 м шляху при виключеному двигуні з постійною швидкістю u=50 км/год. Яку потужність повинен розвивати двигун цього автомобіля, щоб на гору з тим же уклоном автомобіль рухався з тією ж швидкістю?(11,8кВт) 26. Яку механічну роботу виконує маховик з радіусом R=2 м і вагою 6×104Нпри переході від 10 до 4 об/хв? (11200Дж) 27. Вірьовка довжиною 20 м перекинута через блок. В початковий момент вірьовка висить симетрично відносно вертикальної прямої, що перетинає вісь блока і перебуває в спокої; потім, внаслідок незначного поштовху, починає рухатися по блоку. Чи буде рух вірьовки рівноприскореним? Яка буде швидкість вірьовки, коли вона зійде з блока? Масу і розміри блока не враховувати. (10м/с) 28. Розглянути аналогічну задачу для вірьовки, яка лежить на гладенькому горизонтальному столі і в початковий момент знаходиться в спокої, а потім під дією незначного поштовху починає сповзати з стола.(14м/с) 29. 30. Невагомий стержень, довжина якого дорівнює 1м, може обертатися навколо нерухомої точки 0 (рис.1). На кінцях стержня закріплені два тягарі масами т1 = 6кг і тг =3кг. В початковий момент часу (рис 1) стержень розміщений горизонтально. Потім кінець стержня, на якому закріплено тягар т,, починає опускатися. Яку швидкість матиме тягар в найнижчому положенні? (0,96м/с) 31. Людина стоїть на нерухомому візку і кидає горизонтально камінь масою т =8 кг з швидкістю u1=5м/с. Визначити, яку при цьому людина виконує роботу, якщо маса візка разом з людиною становить М=160 кг. Проаналізувати залежність роботи від маси М. (105Дж) 32. Хлопчик розтягнув пружину на якусь довжину. В цьому положенні пружину перехопив дорослий чоловік і розтягнув її ще на таку ж довжину. В скільки разів робота, виконана дорослим чоловіком, більша?(в три рази) 33. Акробат стрибає в сітку з висоти Н =8 м. На якій граничній висоті h1 над підлогою потрібно натягти сітку, щоб акробат не вдарився об підлогу при стрибку? Відомо, що сітка прогинається на h2= 0,5 м, якщо акробат стрибає в неї з висоти Н2 = 1 м. (1,23м) 34. Спіральна пружина розтягується силою 50Н. Коли пружину розтягує додатково сила в 80Н, то вона видовжується на 20 см. Яка робота виконується при цьому видовженні?(18Дж) 35. В нерухоме сферичне тіло масою М, підвішене на нерозтяжному стержні, закріпленому в підвісі на шарнірі, потрапляє куля масою т. Кут між напрямом польоту кулі і лінією стержня становить a=45°. Удар центральний. Після удару куля застряє в тілі і тіло разом з кулею, відхилившись, піднімається на висоту h відносно початкового положення. Знайти швидкість кулі (М=1 кг, т= 10 г, h =0,2 м). (283м/с) 36.На гладенькому столі лежить більярдна куля вагою Р= 8Н. Горизонтальним поштовхом кия кулю скидають з столу і вона падає на підлогу на відстані l =1 м від краю стола по горизонталі. Висота стола h = 0,8м. Визначити енергію поштовху. Тертя і опору повітря не враховувати.(2,5Дж) 37. З гвинтівки зроблено в горизонтальному напрямі два постріли в щит, що знаходиться на відстані S=50 м. Після першого пострілу перед дулом гвинтівки поставили дошку. Друга куля, пробивши дошку, потрапила в щит на d = 0,5 м нижче першої. Яка робота виконана кулею при пробиванні дошки, якщо початкова швидкість кулі u1 =300 м/с? Маса кулі 6г.(163,75 Дж) 38. Визначити кінетичну енергію атомів калію, які вилітають з джерела в горизонтальному напрямі, якщо, пролетівши шлях 2 м, вони під дією сили тяжіння знизилися на 0,5 мм. Атомна маса калію 39.(1,27×10-21Дж) 39. Нейтрон з кінетичною енергією 10-15 Дж поглинається нерухомим ядром кадмію. Визначити швидкість новоутвореного ядра. Атомна маса кадмію 112.(1,06×104м/с) 40. При розпаді одного атома радіоактивного елемента радону (Rn222) з атома вилітає одна a-частинка (атомна маса 4). В результаті атом Rn перетворюється в атом нового елемента RnА. Визначити швидкість віддачі атома RnА, якщо кінетична енергія a-частинки дорівнює 0,8×10-13 Дж. (u=-105м/с) 41. Атом ізотопу урану U 42. При бомбардуванні атомів літію протонами утворюються дві a-частинки. Обчислити їх швидкість, якщо виділення енергії при такій реакції становить 27,2×10 43. Насос заповнює басейн водою за t= 20 сек. Обчислити потужність двигуна насоса, якщо місткість басейна V = 100 м3, його центр знаходиться на висоті h = 18 м над поверхнею води в озері, а коефіцієнт корисної дії насоса 90%.(980кВт) 44. Яку потужність розвиває горизонтальний потік води перерізом S і густиною r, якщо при гальмуванні він змінює свою швидкість від u0 до uрівносповільнено?( 45. 46. Весь шлях автомобіль проїхав із середньою швидкістю 80 км/год. Середня швидкість на першій чверті шляху дорівнювала 120км/год. Яка була середня швидкість на решті шляху?(72 км/год). 47. Рух двох матеріальних точок визначається рівняннями: х1= А1+В1t+С1t2, х2 = А2+В2t+С2t2 де А1= 20м; А2 =2м; В2=В1=2м/с; С1= -4м/с2; C2=0,5м/с2. В який момент часу швидкості цих точок будуть однаковими? Визначити швидкості u 1 та u 2 і прискорення а1 та а2 точок в цей момент (0,2м/с; 2 м/с; -8 м/с2; 1м/с2). 48. Тіло кинуте вертикально вгору з початковою швидкістю 20 м/с. Через 1 с після цього кинуто вертикально вгору друге тіло з такою ж швидкістю. На якій висоті вони зустрінуться? (19,2 м). 49. Матеріальна точка рухається по колу радіусом 4 м. Рівняння її руху S= А+Вt + Сt2, де А= 10м; В= -2 м/с; С=1 м/с2. Знайти тангенціальне, нормальне та повне прискорення точки в момент часу t=4с (2 м/с2; 1 м/с2; 2,24 м/с2). 50. Тіло кинуте з вежі зі швидкістю 30 м/с. Знайти швидкість, тангенціальне та нормальне прискорення тіла в кінці другої секунди після початку руху (35,8 м/с; 5,37 м/с2; 8,22 м/с2). 51. Шків радіусом 20 см обертається з прискоренням. Рівняння його руху j= А+Вt+Сt2, де А=3 рад, В=- 1рад/с, С= 0,1рад/с. Знайти тангенціальне, нормальне та повне прискорення для точок кола шківа для моменту часу t=10с (1,2 м/с2; 168 м/с2; 168 м/с2). 52. Шків обертається з кутовим прискоренням -2 рад/с2. Яку кількість обертів зробить шків, якщо частота обертів зміниться від 240 хв-1 до 90 хв-1? Знайти час, за який це відбудеться (21,6; 7,85 с) 53. Першу половину шляху автомобіль рухався зі швидкістю 72 км/год, а другу половину шляху - зі швидкістю 36 км/год. Визначити середню швидкість руху автомобіля (48км/год). 54. Першу половину часу свого руху автомобіль рухався зі швидкістю 72км/год, а другу половину шляху - зі швидкістю 36 км/год. Визначити середню швидкість руху автомобіля (54км/год). 55. Першу половину шляху тіло пройшло за 2 с, а другу - за 8 с. Визначити середню швидкість тіла, якщо довжина шляху -0,2 км (2 м/с). 56. Три чверті свого шляху автомобіль рухався зі швидкістю 60 км/год, а останню - зі швидкістю 80 км/год. Визначити середню Швидкість автомобіля (64 км/год). 57. Одну третину шляху автомобіль рухався зі швидкістю 80 км/год, а останню частину шляху - зі швидкістю 40 км/год. Визначити середню швидкість автомобіля (48км/год), 58. Першу чверть шляху потяг пройшов зі швидкістю 60 км/год. Середня швидкість на всьому шляху становила 40 км/год. Визначити, з якою швидкістю потяг пройшов решту шляху (u=14,8м/с). 59. Тіло рухалось 15с зі швидкістю 18км/год, 10с зі швидкістю 28,8км/год і 6 с зі швидкістю 72 км/с. Визначити середню швидкість тіла (u=8,87м/с). 60. Першу третину шляху автомобіль, проїхав із швидкістю 28,8 км/год, а останню - з швидкістю 72 км/год. Визначити середню швидкість автомобіля на всьому шляху (u = 8 м/с). 61. Першу третину шляху автомобіль, проїхав із швидкістю 18 км/год, а останню - з швидкістю 28,8 км/год. Визначити середню швидкість автомобіля на всьому шляху ( u6,7 м/с). 62. Першу третину шляху автомобіль рухався зі швидкістю 10 км/год, а другу - з швидкістю 20 км/год. Визначити середню швидкість автомобіля на всьому шляху (u=5 м/с). 63. Яка допустима максимальна швидкість приземлення парашутиста, якщо людина здатна безпечно стрибати з висоти до 2 м? (6,2 м/с). 64. З якої висоти впало тіло, якщо останні 1 м свого шляху воно пройшло за 1с?( 65. Камінь кинули з висоти 1200 м. Який шлях пролетів камінь за останню секунду свого падіння? (150 м). 66. З якої висоти впало тіло, якщо останні 20м свого шляху воно пройшло за 2 с? (20 м,). 67. З одного й того самого місця почали рухатись рівноприскорено в одному напрямі два тіла, при чому друге тіло почало свій рух через 2 с після першого. Перше тіло рухалось з початковою швидкістю 1 м/с і прискоренням 2 м/с2, друге - з початковою швидкістю 10 м/с і прискоренням 1 м/с2. Через який проміжок часу і на якій відстані від початкового положення друге тіло наздожене перше? (Зустрінуться два рази: через 3,4 с на відстані 15 м та через 10,6 с на відстані 123м). 68. Літак летить із пункту А до пункту В, який розташований на сході за 150 км, і в зворотному напрямі. Визначити час, за який пролетить літак цю відстань, якщо: а) вітру немає; б) вітер дме з півдня на північ; в) вітер дме з заходу на схід. Швидкість вітру 20 м/с, швидкість літака відносно вітру -360км/год. (а) 0,83год; б) 0,85год; в) 0,87год). 69. З аеростата, який розташований на висоті 300 м, впав камінь. Через який час камінь долетить до Землі, якщо: 1) аеростат піднімається зі швидкістю 5 м/с; 2) аеростат спускається зі швидкістю 5 м/с; 3) аеростат нерухомий. Опір повітря не враховувати. (1) 8,3 с; 2) 7,3 с; 3) 7,8 с.) 70. Матеріальна точка, переміщуючись з постійним прискоренням, проходить послідовно два відрізки шляху 10 м кожний. Перший відрізок шляху був пройдений за t1= 1.05 с, а другий - за t2 - 2,2 с. Знайти прискорення матеріальної точки та її швидкість uна початку першого відрізку шляху (3,04м/с2; 11,2м/с). 71. З балкону, розташованого на висоті 25 м над поверхнею Землі, кинули вертикально вгору м'ячик із швидкістю 20 м/с. Написати формулу залежності координати від часу, вибравши за початок відліку: а) точку кидання; б) поверхню Землі. Визначити, через який час м'ячик упаде на Землю (5 с). 72. З вежі кинули камінь у горизонтальному напрямку. Через 2 с камінь впав на Землю на відстані 40 м від основи вежі. З якою швидкістю він впаде на Землю? (28 м/с). 73. З балкону кинули м'яч вертикально вгору з початковою швидкістю 5 м/с. Через 2 с м'яч впав на Землю. Визначити висоту балкона над Землею і швидкість м'яча в момент удар)' об Землю (9,62 м; 14,6 м/с). 74. Залежність шляху, пройденого тілом, від часу дається рівнянням S==A+Bt+Ct2+Dt3 де С = 0,14 м/с2 і D= 0,01 м/с3. Через який час після початку рух)' тіло буде мати прискорення 1 м/с2? Знайти середнє прискорення тіла за цей проміжок часу. (3м/с2). 75. Тіло рухається згідно рівняння S= 4t2+2t3+7,м. Визначити швидкість і прискорення тіла в момент часу t - 2 с і середню швидкість за перші 2 с руху (40 м/с; 32 м/с; 19,5 м/с). 76. Тіло рухається згідно рівнянь х =7+ 4t, у=2+3×t. Визначити швидкість руху тіла. (5м/с). 77.Тіло рухається прямолінійно згідно рівняння х = Аt +Вt2, де А=2 м/с; В=- 0,5 м/с2. Визначити середню швидкість руху тіла в інтервалі часу від? t =1 с до t2= 3с.(0,5м/с). 78. Тіло рухається по колу радіусом 4 м згідно рівняння S=A+Bt+Ct2? де А =10 м; B= -2 м/с; С = 1 м/с2. Визначиш тангенціальне, нормальне та повне прискорення в момент часу t= 2 с (2 м/с2; 1 м/с2; 2,24 м/с2). 79. Матеріальна точка рухається по колу так, що залежність шляху, пройденого тілом, від часу задається рівнянням S= А-Bt + Сt2, де В =2м/с і С=1м/с2. Знайти лінійну швидкість точки, її тангенціальне, нормальне та повне прискорення через 3 с після початку руху, якщо через 2 с після початку руху нормальне прискорення точки становило 0,5 м/с. (4 м/с; 2 м/с; 2 м/с; 2,83 м/с2). 80. Визначити кутове прискорення колеса, якщо відомо, що через 2 с після початку рівноприскореного руху вектор повного прискорення точки, яка лежить на ободі, утворює кут 60° з напрямом лінійної швидкості цієї точки. (0,43 м/с2). 81. Матеріальна точка рухається по колу радіусом 2 см. Залежність шляху, пройденого тілом, від часу задається рівнянням S= Сt, де С= 0,1 см/с. Знайти нормальне і тангенціальне прискорення точки в той момент, коли лінійна швидкість точки 0,3м/с. (0,005 см/с2; 0). 82. Колесо радіусом 10 см обертається з постійним кутовим прискоренням 3,14 рад/с2. Знайти для точок обода колеса на кінець першої секунди після початку руху: кутову швидкість; лінійну швидкість; тангенціальне прискорення.(3,14с1; 31,4×10-2 м/с; 31,4×10-2 м/с2). 83. Маховик, який знаходиться в стані спокою, почав обертатись рівноприскорено. Зробивши 200 обертів, він мав кутову швидкість 62.8 с-1 Визначити кутове прискорення маховика під час його рівноприскореного обертання (1,67 с-2). 83. Місяць обертається навколо Землі з періодом 27 діб. Середній радіус орбіти Місяця - 4×105 км. Визначити лінійну швидкість руху Місяця навколо Землі і його нормальне прискорення (3880 км/год; 40 км/год2). 84. Гвинт літака робить 1500 об/хв, при гальмуванні він став обертатись рівносповільнено і зупинився через 30 с. Визначити кутове прискорення і кількість обертів, яку робить гвинт з початку гальмування до остаточної його зупинки (5,42 с-2; 375 обертів). 85. Колесо обертається з кутовим прискоренням 0,5 с -2. Визначити повне прискорення точки, яка розташована на відстані 40 см від осі, через 2 с після початку обертання (0,448 м/с2). 86. Знайти кутові швидкості: а) добового обертання Землі; б) годинникової стрілки годинника; в) хвилинної стрілки годинника; г) обертання Місяця навколо Землі, якщо період обертання Місяця навколо Землі - 27 діб. (а) 7,26×105 с-1; б) 1,74-10-5 с-1; в) 0,1 с-1; г) 2,61×10-6 с-1). 87. Тіло кинуте під кутом до горизонту. Визначити кут, якщо віддаль тіла по горизонталі більша в 4 рази від максимальної висоти траєкторії. Опір повітря не враховувати (14°). 88. Колесо радіусом 5 см обертається так, що залежність кута оберту радіуса колеса від часу задається рівнянням j= А+Bt+Сt2+Dt3,де B=1рад/с3. Знайти, на скільки зміниться тангенціальне прискорення за одиницю часу (0,3м/с2). 89. Колесо, яке обертається рівноприскорено, через час 1 хв після початку обертання набуло частоти 720 об/хв. Знайти кутове прискорення колеса і число обертів колеса за цей час (1,26 с-2; 360 об.) 90. Колесо обертається так, що залежність кута оберту радіуса колеса від часу задається рівнянням j= А+Bt+Сt2+Dt3 де B=1рад/с; С= 1 рад/с2; D = 1 рад/с3. Знайти радіус колеса, якщо відомо, що в кінці другої секунди точки, Що лежать на ободі колеса мають нормальне прискорення аn = 346 м/с2. (1,2 м). 91. Матеріальна точка рухається по криволінійній траєкторії. Тангенціальне прискорення стале і дорівнює 0,5 м/с2. Знайти повне прискорення точки на відрізку траєкторії з радіусом 3 м, якщо точка рухається по цьому відрізку з швидкістю 2 м/с. (1,42 м/с2). 92. Колесо, яке обертається рівноприскорено, після початку обертання набуло кутову швидкість 20 м/с2 через 10 обертів. Знайти кутове прискорення колеса, якщо wо=0. (3,2 с-2). 93. Точки розташовані на відстані 10 см від осі диска і мають лінійну швидкість 3 м/с. Яку кількість обертів в секунду робить диск? (4,8 об/с). 94. Маховик обертається з частотою 10 об/с. При гальмуванні він почав обертатися рівносповілнено і через 12 с зупинився. Яку кількість обертів зробив маховик від початку гальмування до зупинки? (120 обертів). 95. Маховик із стану спокою почав рівноприскорено обертатися і після 40 обертів почав обертатися зі сталою кутовою швидкістю з частотою 8 об/с. Визначити кутове прискорення маховика. (0,1 с-2), 96. Диск радіусом 20 см обертається згідно рівнянню j= А+Bt+Сt2, де А=3 рад; В= -1рад/с; С =0,1рад/с2. Визначити тангенціальне, нормальне і повне прискорення точок по колу диска для моменту часу 10с. (1,2м/с2; 168 м/с2;»168м/с2). 97. Диск радіусом 1 см, який знаходився в стані спокою, почав обертатися з постійним кутовим прискоренням 0,5 с-2. Визначити нормальне, тангенціальне і повне прискорення точок на колі диска в кінці другої секунди після початку обертання. (5×10-2 м/с2; 0,1 м/с2; 11×10 -2 м/с2). 98. Маховик почав обертатися рівноприскорено і за проміжок часу 10 с досяг частоти обертання 300 об/хв. Визначити кутове прискорення маховика та число обертів, які маховик зробив за цей час. (e=2pn/Dt=3.14c-2, N= 99. Камінь кинули з вежі в горизонтальному напрямку зі швидкістю 30м/с. Визначити нормальне прискорення каменя в кінці другої секунди після початку руху. (8,3 м/с2). 100. Тіло обертається рівноприскорено з початковою кутовою швидкістю 5с-1 і кутовим прискоренням 1с-2. Яку кількість обертів робить тіло за 10 с? (16 об). 101. Тіло рухається по колу радіусом 2 см. Залежність шляху від часу дається рівнянням S =Сt3, де С =0,1см/с2. Визначити прискорення тіла в момент, коли лінійна швидкість тіла 0,3 м/с. (an =4,50 м/с2; аt =0,06 м/с2). 102. Колесо, обертаючись рівносповільнено, змінило свою частоту n1=300oб/хв до n2 = 180об/хв за 1 хв. Визначити кутове прискорення колеса та число обертів колеса за цей час. (e= -0,2 м/с2; N=240 об.). 103. Колесо обертається із сталим кутовим прискоренням 2с-2. Через 0,5с після початку руху повне прискорення колеса стало дорівнювати а= 13,6см/с2. Знайти радіус колеса. (6,1 м). 104. Матеріальна точка рухається по колу радіусом 2 м згідно рівнянню S= Аt+Bt3, де А =8м/с; В= -0,2 м/с2. Знайти швидкість, тангенціальне, нормальне і повне прискорення в момент часу t= 3 с. (13,4 м/с; 3,6 м/с2; 90 м/с2; 90 м/с2). 105. Матеріальна точка рухається по колу радіусом 80 см відповідно до рівняння s=10t-0.1t3 (відстань в метрах, час - в секундах). Знайти швидкість, тангенціальне, нормальне і повне прискорення в момент часу t = 2с. (8,8м/с; аt= - 1,2 м/с; аn =96,8м/с; а = 96,8 м/с2).
107. Два однакових тіла масою М зв'язані між собою ниткою, перекинутою через блок з нерухомою віссю. На однієї з тіл кладуть тягарець масою т. Визначити: 1) 3 яким прискоренням рухатимуться тіла? 2) Який буде натяг нитки при русі тіл? 3) Який тиск на вісь блока створюватиме нитка? 4) 3 якою силою тиснутиме тягарець т на тягар М? Масу блока, вагу нитки і опір повітря не враховувати.(а= m×g×(m+2×M), f=2×m×M×g/(m+2M).) 108. До кінців нитки, перекинутої через нерухомий блок, підвішені два тіла вагою Р1=10Ні Р 2 =20Н. З яким прискоренням рухатимуться тіла і з якою силою при цьому натягуватиметься нитка? (FH=4/3×P1.) 109.З яким прискоренням рухатиметься тіло вагою Р1=10Н, якщо до другого кінця нитки замість тіла вагою Р2 = 20Н прикласти силу в F = 20Н? Масу блока і тертя в розрахунки не приймати. (a=g/3,) 110. На нитці, що витримує натяг 10 Н, піднімають тягар вагою в 5 Нз стану спокою вертикально вгору. Вважаючи рух рівноприскореним і силу опору рівною в середньому 1Н,знайти максимальну висоту, на яку можна підняти тягар за 1стак, щоб нитка не порвалась.(3.92м) 111. Два тіла з масами т1 = 50 г і m 2 = 100 г зв'язані ниткою і лежать на гладенькій горизонтальній поверхні. З якою силою можна тягнути перше тіло, щоб нитка не порвалася, якщо вона витримує навантаження Fн = 5Н? Чи зміниться результат, якщо силу прикласти до другого тіла?(7,5Н; 15Н) 112. Автодрезина веде дві платформи з вантажем, розвиваючи при цьому силу тяги 800Н. Маса першої платформи 12 т,другої - 8 т. З якою силою натягується зчеплення між платформами?(320Н). 113. Краплина дощу, падаючи з великої висоти, випаровується. Як впливає це випаровування на рух краплини? (швидкість стає меншою). 114. Через блок, вісь якого горизонтальна, перекинута вірьовка довжиною l. За кінці вірьовки тримаються два хлопці, що знаходяться на однакових відстанях 115. До кінця нитки, перекинутої через нерухомий блок, прикріплено тягар Q= 20 Н, на другому кінці нитки знаходиться рухомий блок, до якого прикріплено тягар Р = 60Н. Визначити прискорення кожного тіла і розтяг нитки. Тертя і масу блоків не враховувати.?(2,8м/с2, -1,4м/с2, 25,7Н) 116. Вірьовка довжиною 12 м і вагою 60Нперекинута через блок і ковзає по ньому без тертя. Чому дорівнює натяг в середині вірьовки в той момент, коли довжина вірьовки по одну сторону блока дорівнює 8 м? (20Н) 117. Через легкий блок, що може рухатися без тертя, перекинута нитка. На одному кінці нитки прив'язано тягар масою М. По другому кінцю нитки з постійним відносно нитки прискоренням а 2 ковзає кільце масою т. Визначити прискорення а1 тягаря масою М і силу тертя FТ кільця по нитці. Масою нитки нехтувати.( 118. Вірьовка витримує тягар в 900 Н при вертикальному підніманні його з деяким прискоренням і тягар в 1100 Н при опусканні з таким же прискоренням. Який тягар можна піднімати за допомогою цієї вірьовки рівномірно? (990Н) 119. Парашутист, пролетівши відстань в 20 м як вільно падаюче тіло, розкрив парашут і за 3 сзменшив швидкість в 10 раз. Визначити натяг тросів при сповільненому русі парашутиста, якщо вага його 600 Н. (960Н) 120. 121. Два зв'язані один з одним ниткою тягарі рухаються вниз з прискоренням, вдвоє більшим за прискорення вільного падіння. У скільки разів натяг Fн нитки, за яку тягнуть обидва тягарі, більший від натягу F’н нитки, яка зв'язує тягарі? Маса нижнього тягаря в три рази більша від маси верхнього тягаря.(в 4 рази) 122. Два однакових тіла А і В масою т зв'язані ниткою і знаходяться на різних схилах похилої площини, як це показано на (рис.4). Коефіцієнти тертя становлять відповідно k1 і k2, кути нахилу a і b. Тіло В починає ковзати вниз. З яким, прискоренням будуть рухатися тіла А і В?( 123. На верхньому кінці похилої площини закріплено блок, через який перекинуто нитку. До одного кінця нитки прив'язано тягар масою т1 = 2 кг, що лежить на похилій площині. На другому кінці нитки висить тягар масою m 2= 1кг. Похила площина утворює з горизонтом кут a= 20°; коефіцієнт тертя між тягарем т1 і похилою площиною k = 0,1. З яким прискоренням рухаються тягарі і з якою силою натягується нитка? (0,418м/с2, 9,39Н)
124. Яку найбільшу силу тяги можна прикласти до нижнього бруска (рис.5), щоб верхній брусок утримувався на поверхні бруска Р2 в рівноприскореному русі? Коефіцієнт тертя для верхнього бруска k1 = 0,1 і для нижнього бруска k 2 =0,2. Вага верхнього бруска Р1 =10Н і нижнього Р 2=20Н. (9Н) 125. На два бруски масами т1 і m 2, зв'язані нерозтяжною ниткою, діють сили F1 і F2 під кутами a i b до горизонту (рис.6). Знайти прискорення системи, якщо коефіцієнт тертя між брусками і горизонтальною площиною дорівнює k. ( 126. Тягар вагою Р за допомогою нитки, перекинутої через невагомий блок, тягне по похилій площині тягар такої ж ваги (рис. 7). Визначити прискорення, з яким рухаються тягарі, якщо похила площина утворює з горизонтом кут a=30°, а коефіцієнт тертя k = 0,05.(2,2м/с2) 127. 128. До тягаря А масою 7 кг підвішені на вірьовці тягар В масою 5 кг. Маса вірьовки 4 кг. До тягаря А прикладена напрямлена вгору сила 240 Н. Знайти натяг у верхньому кінці вірьовки і в її середині.(135Н, 105Н) 129. 130. Для рівномірного піднімання вантажу вагою Р = 1000 Нпо похилій площині, яка утворює кут 60° з вертикаллю (рис. 8), треба прикладати силу F =600Н. З яким прискоренням рухатиметься вантаж вниз, якщо його відпустити? (3,92м/с2) 131. Стовп масою 200 кг тягнуть з постійною швидкістю силою 50 Нза допомогою вірьовки довжиною l =4 м. Відстань вільного кінця вірьовки від землі h= 0,75 м. Вірьовка прикріплена до центра ваги стовпа (рис.9). Визначити коефіцієнт тертя стовпа по поверхні землі. Чи зміниться величина сили тертя, якщо вірьовка буде прикріплена до кінця стовпа?(0,025, ні.)
132. Тіло з густиною 800 кг/м3 занурили на 1 м під поверхню води і відпустили. На яку максимальну висоту над поверхнею води воно підніметься? Тертя тіла об повітря і воду не враховувати, а також нехтувати густиною повітря.(0,25м) 133. До стелі ліфта, що піднімається з прискоренням a 0 =1,2м /сек2,прикріплено динамометр, до якого підвішений блок, що вільно обертається навколо горизонтальної осі. Через блок перекинута нитка, до кінців якої прикріплені тягарі масою т1 =200 г і m 2=300 г. Нехтуючи масою блока, визначити показання динамометра.(5,28Н) 134. Тепловоз вагою Р =5×105Н тягне состав з п =20 навантажених вагонів. Вага кожного вагона дорівнює вазі тепловоза. Визначити час, протягом якого состав, рушивши з місця, набуде швидкості u=36 км/год. Сила тяги тепловоза F= 6×104 м; коефіцієнт тертя k =0,005.(18хв.) 135. На столі лежить брусок вагою 50Н.До бруска за допомогою нитки, перекинутої через блок (рис. 10), прив'язаний тягар вагою 10Н. Коефіцієнт тертя між поверхнями бруска і стола дорівнює 0,4. Тоді сила тертя, прикладена до бруска і напрямлена вліво, дорівнює 0,4×50Н=20Н. Звідси виходить, що брусок повинен почати рухатися вліво, тому що сила тертя на 10Н більша за вагу тягаря. Відшукати помилку в міркуваннях. 136. В певний момент часу t поїзд має швидкість 36 км/год. Сила тяги електровоза дорівнює 21×104Н; вага поїзда 5×106 Н. Коефіцієнт тертя 0,002 вважати постійним. Визначити швидкість, яку поїзд матиме через 10спісля моменту t, і шлях, який він пройде за ці 10с(13,92м/с, 119,6м).
138. На горизонтальній дошці лежить тягар. Коефіцієнт тертя між дошкою і тягарем 0,1. Яке прискорення в горизонтальному напрямі слід надати дошці, щоб тягар міг ковзати з дошки?(а >0.98м/с2) 139. Два однакових тіла зв'язані ниткою і лежать на
|

 =0,8. Визначити силу тяги, яку розвиває електропоїзд.(48000Н)
=0,8. Визначити силу тяги, яку розвиває електропоїзд.(48000Н)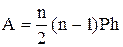 )
) )
)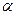 =1°, причому двигун локомотива виключений. Який відрізок шляху пройде поїзд по похилому шляху до моменту зупинки, якщо коефіцієнт тертя k= 0,004 (інші опори не враховувати)? Яку мінімальну потужність повинен розвивати двигун локомотива, щоб при в'їзді на уклон рух поїзда залишився рівномірним?(2135м, 5057кВт)
=1°, причому двигун локомотива виключений. Який відрізок шляху пройде поїзд по похилому шляху до моменту зупинки, якщо коефіцієнт тертя k= 0,004 (інші опори не враховувати)? Яку мінімальну потужність повинен розвивати двигун локомотива, щоб при в'їзді на уклон рух поїзда залишився рівномірним?(2135м, 5057кВт) . Потім тіло кидають в напрямі руху поїзда з швидкістю uвідносно поїзда, надаючи йому таким чином енергії
. Потім тіло кидають в напрямі руху поїзда з швидкістю uвідносно поїзда, надаючи йому таким чином енергії 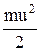 Отже, тіло буде мати енергію
Отже, тіло буде мати енергію 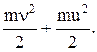 Можна міркувати і так: тіло рухається відносно землі з швидкістю u + и, отже, має енергію
Можна міркувати і так: тіло рухається відносно землі з швидкістю u + и, отже, має енергію 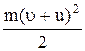 . Цей вираз більший за попередній на m×u×u. Яке з цих міркувань неправильне?
. Цей вираз більший за попередній на m×u×u. Яке з цих міркувань неправильне? 
 На кінцях і посередині невагомого стержня довжиною l розміщені однакові кульки. Стержень ставлять вертикально на гладеньку горизонтальну поверхню і відпускають. Визначити швидкість верхньої кульки в момент її удару об горизонтальну площину. Якою буде ця швидкість, якщо нижній кінець стержня шарнірно закріплений?(
На кінцях і посередині невагомого стержня довжиною l розміщені однакові кульки. Стержень ставлять вертикально на гладеньку горизонтальну поверхню і відпускають. Визначити швидкість верхньої кульки в момент її удару об горизонтальну площину. Якою буде ця швидкість, якщо нижній кінець стержня шарнірно закріплений?(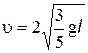 )
)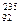 ділиться за схемою
ділиться за схемою 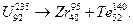 При розпаді звільняється енергія 5×10-11 Дж. Чому дорівнює швидкість утвореного в результаті поділу ядра
При розпаді звільняється енергія 5×10-11 Дж. Чому дорівнює швидкість утвореного в результаті поділу ядра 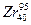 ?(1,92×107м/с)
?(1,92×107м/с)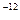 Дж. Енергію налітаючого протона не враховувати.(6,3×107м/с)
Дж. Енергію налітаючого протона не враховувати.(6,3×107м/с) )
) Колесо водяного млина з плоскими радіальними лопатнями приводиться в обертальний рух ударом струменя води (рис. 2). При якій кутовій швидкості обертання колеса ККД його буде максимальний, якщо швидкість води в струмині становить u і струмина потрапляє в лопать на відстані R від осі обертання колеса? (w=u/3R)
Колесо водяного млина з плоскими радіальними лопатнями приводиться в обертальний рух ударом струменя води (рис. 2). При якій кутовій швидкості обертання колеса ККД його буде максимальний, якщо швидкість води в струмині становить u і струмина потрапляє в лопать на відстані R від осі обертання колеса? (w=u/3R)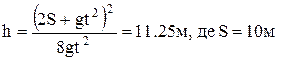 ).
).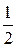 nDt=25).
nDt=25). 106. На гладенькій горизонтальній площині знаходиться тіло масою М (рис.3). Друге тіло масою m підвішене на нитці, перекинутій через блок і прив'язаній до тіла маси М. Визначити прискорення системи і натяг нитки. Тертям тіла маси М по площині і тертям в блоці, а також масами блока і нитки нехтувати.(а= m×g×(m+M), FH= m×M×g/(m+M).)
106. На гладенькій горизонтальній площині знаходиться тіло масою М (рис.3). Друге тіло масою m підвішене на нитці, перекинутій через блок і прив'язаній до тіла маси М. Визначити прискорення системи і натяг нитки. Тертям тіла маси М по площині і тертям в блоці, а також масами блока і нитки нехтувати.(а= m×g×(m+M), FH= m×M×g/(m+M).)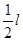 від блока. Хлопчики починають одночасно підніматися вгору, причому один з них рухається відносно вірьовки з швидкістю u, а другий — з швидкістю 2 u. Через який час кожний з хлопчиків досягне блока? Масою блока і вірьовки нехтувати. Маси хлопчиків однакові.(t=l /3u).
від блока. Хлопчики починають одночасно підніматися вгору, причому один з них рухається відносно вірьовки з швидкістю u, а другий — з швидкістю 2 u. Через який час кожний з хлопчиків досягне блока? Масою блока і вірьовки нехтувати. Маси хлопчиків однакові.(t=l /3u). )
) На тіло масою m, що знаходиться на горизонтальній площині, діє сила під кутом а до горизонту. Визначити величину цієї сили, якщо тіло рухається горизонтально з прискоренням а. Коефіцієнт тертя k(.
На тіло масою m, що знаходиться на горизонтальній площині, діє сила під кутом а до горизонту. Визначити величину цієї сили, якщо тіло рухається горизонтально з прискоренням а. Коефіцієнт тертя k(. 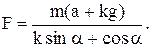 )
)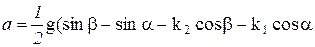 ).
).
 )
) При умовах руху тягарів, описаних в попередній задачі, знайти силу, що діє на блок, якщо т=1 кг. (13Н)
При умовах руху тягарів, описаних в попередній задачі, знайти силу, що діє на блок, якщо т=1 кг. (13Н) Тіло вільно ковзає з вершини нерухомої похилої площини під кутом a=30° до горизонту. Визначити його швидкість в кінці похилої площини і час руху, якщо висота похилої площини h =10 м, а коефіцієнт тертя k =0,05.(14м/с, 3с)
Тіло вільно ковзає з вершини нерухомої похилої площини під кутом a=30° до горизонту. Визначити його швидкість в кінці похилої площини і час руху, якщо висота похилої площини h =10 м, а коефіцієнт тертя k =0,05.(14м/с, 3с)
 137. Великий балон, заповнений газом під тиском, повернутий горлом вниз (рис. 11). Якщо звільнити поршень від сил, що його утримують, то поршень виштовхується стисненим газом, щоб прискорити виліт поршня з балона, пропонуються два способи: а) покласти на поршень зверху гирю; б) припаяти до пробки тягар такої ж маси, що й у гирі. Який спосіб кращий? Тертя не враховувати.
137. Великий балон, заповнений газом під тиском, повернутий горлом вниз (рис. 11). Якщо звільнити поршень від сил, що його утримують, то поршень виштовхується стисненим газом, щоб прискорити виліт поршня з балона, пропонуються два способи: а) покласти на поршень зверху гирю; б) припаяти до пробки тягар такої ж маси, що й у гирі. Який спосіб кращий? Тертя не враховувати.


