Основні формули
Закон Кулона
де F — сила взаємодії точкових зарядів Q 1 Q 2; r –відстань між зарядами; e– проникливість; e0 – електрична постійна. Напруженість електричного поля і потенціал
де П—потенційна енергія точкового додатного заряду Q, який є в даній точці поля (за умови, що потенційна енергія заряду, віддаленого в нескінченність, дорівнює нулю). Сила, яка діє на точковий заряд, що є в електричному полі, і потенційна енергія цього заряду
Напруженість і потенціал поля, створеного системою точкових зарядів (принцип суперпозиції електричних полів),
де Е, j; — напруженість і потенціал у даній точці поля, створеного і -м зарядом. Напруженість і потенціал поля, створеного точковим зарядом,
де r – відстань від заряду Q до точки, у якій визначається напруженість і потенціал. Напруженість і потенціал поля, створені провідною зарядженою сферою радіусом R на відстані r від центра сфери: а). б) с) де Q — заряд сфери. Лінійна густина заряду
Поверхнева густина заряду
Напруженість і потенціал поля, створеного розподіленими зарядами. Якщо заряд рівномірно розподілений уздовж лінії з лінійною густиною, t то на лінії виділяється мала ділянка довжиною d l із зарядом dQ = t d l,і такий заряд можна розглядати як точковий та використовувати формули:
де r – радіус-вектор, спрямований від виділеного елемента dl до точки, в якій визначається напруженість. Використовуючи принцип суперпозиції електричних полів знаходимо інтегруванням напруженість Е і потенціал j поля, створеного розподіленим зарядом:
Інтегрування ведеться вздовж усієї довжини l зарядженої лінії (див. приклади 5 і 8). Напруженість поля, утвореного нескінченою прямою рівномірно зарядженою лінією чи нескінченно довгим циліндром,
де r – відстань від прямої чи осі циліндра до точки, в якій визначається напруженість поля. Напруженість поля, утвореного нескінченно рівномірно зарядженою площиною,
Зв’язок між потенціалом і напруженістю: а) б) в) Електричний момент диполя
де l – плече диполя (векторна величина, що спрямована від від’ємного заряду до додатного і чисельно дорівнює відстані між зарядами), q – заряд. Робота сил електричного поля переміщення заряду q з точки поля з потенціалом
Електроємність
де - j потенціал провідника (при умові, що у нескінченності потенціал провідника дорівнює нулю); U - різниця потенціалів пластин конденсатора. Електроємність плоского конденсатора
де S - площа пластини (однієї) конденсатора; d - відстань між пластинами.
Електроємність батареї конденсаторів: а) б) де N – кількість конденсаторів у батареї. Енергія зарядженого конденсатора:
Сила постійного струму:
де q – заряд, що пройшов через поперечний перетин провідника за час t. Густина постійного струму:
де S – площа поперечного перетину провідника. Зв’язок густини струму з середньою швидкістю -u;
де q – заряд частинки; n – концентрація заряджених частинок. Закон Ома: а) б) в) Закони Кірхгофа: а) б) де Опір R і провідність G провідника
де Опір системи провідників: а) б) де Робота струму:
Перша формула справедлива для будь-якої ділянки ланцюга, на кінцях якого підтримується напруга U, останні дві - для ділянки, що не містить ЕРС. Потужність струму:
Закон Джоуля— Ленца
Закон Ома в диференціальній формі:
де Зв'язок питомої провідності
де q - заряд іона; n - концентрація іонів;
|

 ,
,


 ,
, (при r -R)
(при r -R) (при r -R)
(при r -R) (при r -R)
(при r -R)





 чи
чи  в загальному випадку;
в загальному випадку; у випадку однорідного поля;
у випадку однорідного поля; у випадку поля, яке має центральну чи осьову симетрію.
у випадку поля, яке має центральну чи осьову симетрію. ,
, у точку з потенціалом
у точку з потенціалом 

 чи
чи 
 ,
, при послідовному з’єднані;
при послідовному з’єднані; ,
,



 для ділянки кола в якому немає ЕРС, де -
для ділянки кола в якому немає ЕРС, де -  - різниця потенціалів (напруга) на кінцях ділянок ланцюга; R – опір ділянки;
- різниця потенціалів (напруга) на кінцях ділянок ланцюга; R – опір ділянки; для ділянки кола, що має ЕРС; де
для ділянки кола, що має ЕРС; де  - ЕРС джерела струму; R — повний опір ділянки (сума зовнішніх і внутрішніх опорів);
- ЕРС джерела струму; R — повний опір ділянки (сума зовнішніх і внутрішніх опорів); для замкнутого (повного) ланцюга, де R - зовнішній опір ланцюга; R i - внутрішній опір ланцюга.
для замкнутого (повного) ланцюга, де R - зовнішній опір ланцюга; R i - внутрішній опір ланцюга. - перший закон;
- перший закон; - другий закон,
- другий закон, - алгебраїчна сума сил струмів, що сходяться у вузлі;
- алгебраїчна сума сил струмів, що сходяться у вузлі;  - алгебраїчна сума добутків сил струмів на опори ділянок;
- алгебраїчна сума добутків сил струмів на опори ділянок;  алгебраїчна сума ЕРС.
алгебраїчна сума ЕРС.
 - питомий опір;
- питомий опір;  - питома провідність;
- питома провідність;  - довжина провідника;
- довжина провідника;  - площа поперечного переріза провідника.
- площа поперечного переріза провідника. при послідовному з'єднанні;
при послідовному з'єднанні; при паралельному з'єднанні;
при паралельному з'єднанні;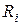 - опір і -го провідника.
- опір і -го провідника.


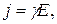
 з рухливістю b заряджених часток (іонів)
з рухливістю b заряджених часток (іонів)
 - рухливості позитивних і негативних іонів.
- рухливості позитивних і негативних іонів.


