Математическая статистика

Теоретическое число тарелок η_{теоретич.}определяется по числу «ступенек», которые строятся, начиная с точки «а» до пересе­чения с вертикалью - X_wРабочее (практическое) число тарелок = n теор.. 1,7

 

 

 

Лабораторная работа № 3

Математическая статистика

 

1. Медиана

Пусть в таблице показан расход электроэнергии в январе жильцами девяти квартир.

Номер квартиры
Расход энергии, кВт*ч

Составим из приведенных данных упорядоченный ряд.

64, 72, 72, 75, 78, 82, 85, 91, 93

В полученном упорядоченном ряду девять чисел. Какое число расположено ровно посередине этого упорядоченного ряда? Это число 78: слева от него стоит четыре числа и справа тоже четыре числа.

Говорят, что число 78 является медианой рассматриваемого упорядоченного ряда (от латинского слова mediana, которое означает «среднее»). Это число можно считать медианой и для исходного (неупорядоченного) ряда чисел.

 

Изменим условие задачи. Пусть при сборе данных о расходе электроэнергии к указанным девяти квартирам добавили еще десятую. Получили новую таблицу

Номер квартиры
Расход энергии, кВт*ч

Также как в первом случае, представим полученные данные в виде упорядоченного ряда чисел:

64, 72, 72, 75, 78, 82, 83, 85, 91, 93.

Попробуйте найти число, которое стоит ровно посередине – медиану – для этого ряда. Получается? Почему?

В этом числовом ряду четное число членов, поэтому имеется два числа, расположенные в середине ряда: это числа 78 и 82. Для того, чтобы найти медиану числового ряда с четным числом членов найдем среднее арифметическое этих двух чисел: . Число 80, не являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы: слева от него находится пять членов ряда, и справа тоже пять членов ряда:

Говорят, что в этом случае медианой рассматриваемого упорядоченного ряда, а также исходного (неупорядоченного ряда) является число 80.

Т.о. медианой произвольного ряда чисел является медиана соответствующего упорядоченного ряда.

 

Определение 1. Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

 

В каждом из рассмотренных выше примеров, определив медиану, мы можем указать номера квартир, для которых расход электроэнергии жильцами превосходит серединное значение, то есть медиану.

 

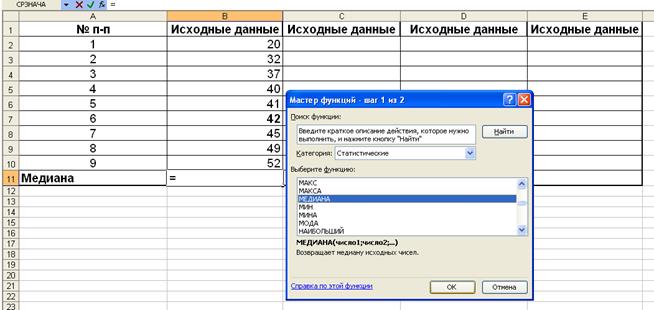
Задание 1. Найдите медиану для четырех рядов чисел

А
Б
В
Г	1,2	1,4	2,2	2,6	3,2	3,8	4,4	5,6

Задание выполнить в редакторе электронных таблиц Microsoft Excel. В одном файле Microsoft Excel каждую задачу выполняем на отдельном листке, которые подписываем«задание 1», «задание 2» и т.д.

 

Задание 2 Найдите среднее арифметическое и медиану рядов чисел.

А
Б
В	3,8	7,2	6,4	6,8	7,2
Г	21,6	37,3	16,4	12,6

 

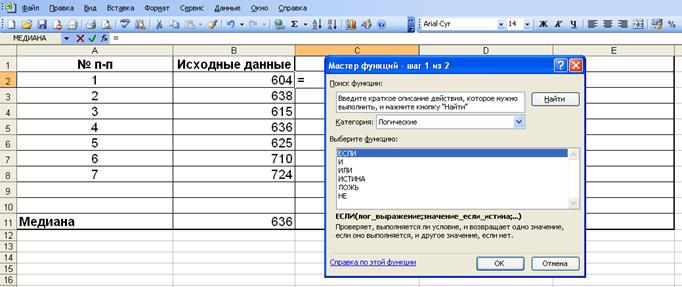
Задание 3. В таблице показано число посетителей выставки в разные дни недели.

День недели	Пн	Вт	Ср	Чт	Пт	Сб	Вс
Число посетителей

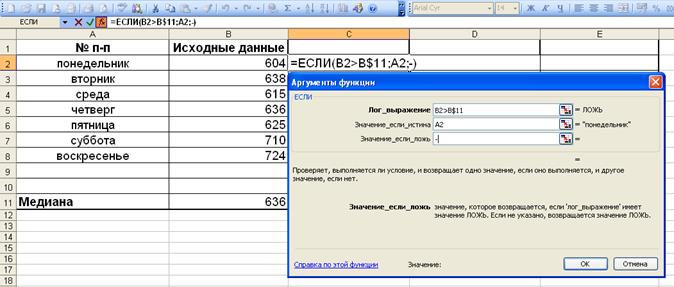
Найдите медиану указанного ряда данных.

В какие дни недели число посетителей выставки было меньше медианы? Для решения этой задачи использовать логическую функцию «ЕСЛИ»

 

 

 

Задание 4. В таблице показано число изделий, изготовленных за месяц членами артели. Найдите медиану этого ряда данных. У кого из членов артели выработка за месяц была больше медианы?

№	Фамилия	Число изделий	№	Фамилия	Число изделий
	Антонов			Квитко
	Астафьев			Лазарев
	Баранов			Осокин
	Боков			Рылов
	Васильев			Сухов
	Егоров			Чернышев

 

Задание 5. В таблице показано, сколько акций одинаковой стоимости некоторого акционерного общества приобрели сотрудники отдела. Найдите медиану этого ряда. У кого из сотрудников отдела число приобретенных акций превосходит медиану?