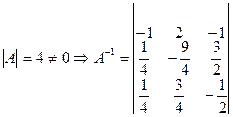Миноры и алгебраические дополнения.
Пусть АÎКm,n.выберем k номеров строк i1,….,ik, и k номеров столбцов j1,…..,jk: i1<i2<…< ik j1<j2<…< jk Def5:минором порядка k матрицы А называется определитель матрицы порядка k,образованной элементами, находящимися на пересечении выбранных строк и столбцов. Обозначение: Примеры: А= Def 6: Если А – квадратная порядка n,то каждому минору Алгебраическими дополнениями минора Если mij=aij =>aij=(-1)i+j Пример: Теорема 1(о разложении определителя) Если АÎКn,n и n>1,то detA равен сумме произведений элементов любой строки матрицы А на их алгебраические дополнения,те detA=ai1Ai1+…+ainAin, "i=1,…n. Доказательство: Пусть A= Покажем, что Лемма 1: А= Доказательство: detA= Рассмотрим tÎSn-1: t
=(-1)i+j Следствие(разложение по чужой строке) Сумма произведений всех элементов какой-нибудь строки определителя на алгебраические дополнения соответствующих элементов другой строки равна нулю. Доказательство: Пусть А= (aij)ÎКn,n.рассмотрим матрицу Пример: 1) |A|= Следующая теорема обобщает теорему 1. Теорема 2(теорема Лапласа) Пусть матрице А порядка n произвольно выбраны k строк,1£k£n-1. Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна detA.Те если i1,…ik – выбранные строки, то detA= где суммирование ведется по всевозможным значениям индексов j1,….jk, 1£j1<j2<…<jn£n Формула (1) называется формулой разложения определителя по k-й строке i1,…ik. Доказательство: см Ильин, Поздяк стр 27 Примеры: 1)
2)
3) Определитель Вандермонда.
Вычитая первый столбец из всех остальных, получаем:
4°. Определитель суммы и произведения матриц. Непосредственно из линейного свойства определителя вытекает: Теорема 1: Если A, B Є Kn, n, то det(A+B) равен сумме определителей матриц порядка n, каждая из которой получается следующим образом: часть строк (столбцов) берутся совпадающими с соответствующими строками (столбцами) матрицы A, а остальные – совпадающие с соответствующими строками (столбцами) матрицы B. Иллюстрация, A,B Є K2, 2. Теорема 2: Если A, B Є Kn, n, то det(AB)=det A·det B Док-во: Рассмотрим матрицу D порядка 2n:
Из примера 1 пункта 3° имеем, что det D=det A·det B. Преобразуем теперь матрицу D. (n+1) строку умножим на a11, (n+2) – на a12, …, 2n-ую –на a1n и сложим с первой строкой. Тогда первая строка имеет вид: (0, …, 0, ¦ a1kbk1 … a1kbkn). Аналогично к i-ой строке прибавим (n+1), умноженную на ai1, (n+2) – на ai2, …, 2n-ую на ain. Имеем: (0, …, 0, ¦ a1kbk1 … a1kbkn). Т.о., первые n строк принимают вид:
При таких преобразованиях определитель не меняется где det C=det A·det B.
Следствие 1: Если A1, …, Ak Є Kn, n Следствие 2: Из 5°. Обратная матрица. Пусть A – квадратная матрица порядка n над полем P. Def1:Матрица В Є Pn, n называется обратной для A, если AB=En.
Def2: Квадратная матрица А называется невырожденной (или неособой), если
Из теоремы 2 пункта 4° Þ произведение матриц, одна из которых вырождена, будет вырожденной матрицей, а произведение двух невырожденных матриц дает невырожденную матрицу.
Def3: Матрицей присоединенной к матрице A, называется матрица
где Aij – алгебраическое дополнение элемента aij матрицы А.
Лемма: Для матриц A и AV справедливо A·AV=AV·A=(detA)·En Док-во: Пусть C= A·AV. Тогда
Итак, A·AV=detA·En. Аналогично AV·A=A·AV= (detA)·En Теорема 1: Для того, чтобы для матрица A существовала обратная, необходимо и достаточно, чтобы матрица А была невырожденной. Док-во: Þ Пусть для матрицы A
Замечание: итак Пример:
Свойства обратных матриц: Пусть A, B Є Pn, n Тогда 1° (A-1)-1=A 2°. (A-1)T=(AT)-1 3°. (A-1)K=(AK)-1 4°. det(A-1)=(detA)-1 5°. (AB)-1=B-1·A-1
|


 ,
,  ,
, 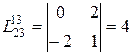
 порядка к можно поставить в соответствие дополнительный минор
порядка к можно поставить в соответствие дополнительный минор  порядка n-k,элементы которого расположены на пересечении остальных строк и столбцов. Очевидно, что минор
порядка n-k,элементы которого расположены на пересечении остальных строк и столбцов. Очевидно, что минор  будет в свою очередь дополнительным к
будет в свою очередь дополнительным к  :
: 

 => А22=(-1)2+2
=> А22=(-1)2+2  =9
=9 .Тогда, выбрав i-ю строку, определитель А можно представить как сумму: detA=
.Тогда, выбрав i-ю строку, определитель А можно представить как сумму: detA=  , где
, где  i-я строка
i-я строка =Aij. Переставляя n-j раз столбцы и n-i раз строки, получим:
=Aij. Переставляя n-j раз столбцы и n-i раз строки, получим: 

 =
=  =
= 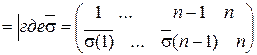 =
=  .
. . Очевидно,что e(t)=
. Очевидно,что e(t)= 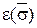 ,так что число инверсий в t и
,так что число инверсий в t и 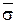 одно и тоже и значит detA=
одно и тоже и значит detA= 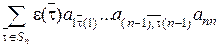 = =
= =  чтд
чтд
 Вернемся к доказательству теоремы:
Вернемся к доказательству теоремы:  =
=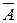 , получающуюся из А заменой i-ой строки на j-ю,оставляя j-ю прежней=>detA=0. Напишем разложение
, получающуюся из А заменой i-ой строки на j-ю,оставляя j-ю прежней=>detA=0. Напишем разложение 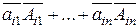 = =
= =  тк алгебраические дополнения к элементам i-ой строки у матрицы А и
тк алгебраические дополнения к элементам i-ой строки у матрицы А и  =
= 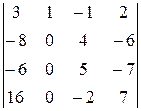 =(-1)
=(-1)  = =2
= =2  =2(-54+140-150+84)=40
=2(-54+140-150+84)=40 (1),
(1),
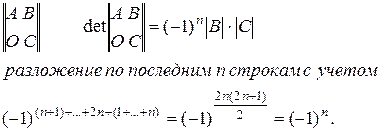


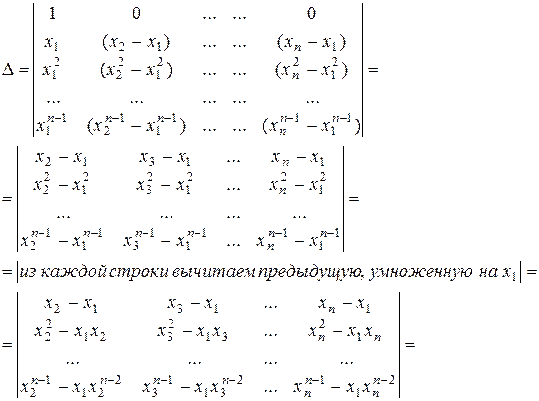

 , где On – нулевая квадратная матрица порядка n,
, где On – нулевая квадратная матрица порядка n,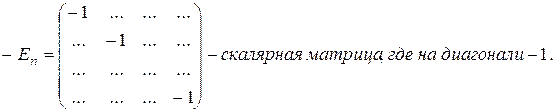
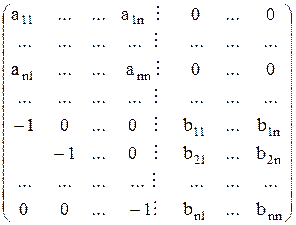


 . Но
. Но 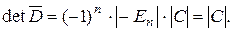 Т.о. доказано, что
Т.о. доказано, что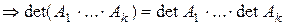

 и вырожденной (особой), если detA=0.
и вырожденной (особой), если detA=0. ,
,