Теорема о базисном миноре матрицы.
1°. Линейная зависимость строк матрицы. Пусть P – поле. Def1 Будем говорить, что строка B=(b1, …, bn) bi Є P является линейной комбинацией строк A1=(a11, …, a1n,), …, Ak=(k1, …, akn,), aij Є P, если для некоторых α1,…, αk Є P справедливо bj=α1aij + … + αkj, j=1, …, n. (1) Это равенство удобно записать в матричном виде: B=α1A1+ … + αkAk. (1’) Def2 Строки A1=(a11, …, a1n,), …, Ak=(k1, …, akn,) назовем линейно зависимыми, если
Строки, не являющиеся линейно зависимыми, являются линейно независимыми. Иными словами, A1, …, Ak – линейно независимы, если равенство Теорема 1: Строки A1, …, Ak – линейно зависимы Док-во:
2°. Теорема о базисном миноре. Рассмотрим матрицу A Є Pm, n, где P-поле матрицы размера m·n Def3 Число r 1) 2) Все миноры (r+1)-го порядка равны нулю. Т.о., рангом матрицы называется порядок наибольшего отличного от нуля минора. Минор r-го порядка, отличный от нуля, называется базисным минором, строки и столбцы, на пересечении которых находится базисный минор, называются базисными строками и базисными столбцами. Теорема 2(теорема о базисном миноре): Базисные строки (столбцы) линейно независимы. Любая строка (любой столбец) матрицы A является линейной комбинацией базисных строк (базисных столбцов). Док-во (Рассуждение для строк): Покажем, что базисные строки линейно независимы Если первая, например, строка – линейная комбинация остальных, то вычитая в базисном миноре из первой строки линейную комбинацию остальных, получим нулевую строку Докажем, что Рассмотрим определитель (r+1) порядка
Здесь Разложим его по r+1 столбцу. Отметим, что
Теорема 3 (необходимое и достаточное условие равенству нулю определителя) Определитель n-го порядка равен нулю Док-во:
|


 такие
такие  одновременно не равные нулю, такие что
одновременно не равные нулю, такие что
 возможно лишь когда
возможно лишь когда 
 одна из этих строк является линейной комбинацией остальных.
одна из этих строк является линейной комбинацией остальных.
 но
но

 0 называется рангом матрицы A, если
0 называется рангом матрицы A, если базисный минор нулевой – противоречие.
базисный минор нулевой – противоречие. строка A является линейной комбинацией остальных. Т.к. при переменах строк и столбцов определитель сохраняет свойство равенства (неравенства) нулю, то будем считать, что базисный минор составлен из первых r строк и r столбцов.
строка A является линейной комбинацией остальных. Т.к. при переменах строк и столбцов определитель сохраняет свойство равенства (неравенства) нулю, то будем считать, что базисный минор составлен из первых r строк и r столбцов.

 Если
Если  то две одинаковые строки или столбца и определитель равны нулю.
то две одинаковые строки или столбца и определитель равны нулю. 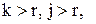 то это минор порядка r+1
то это минор порядка r+1  и коэффициенты Aij не зависят от выбора j, т.е.
и коэффициенты Aij не зависят от выбора j, т.е. 
 что означает, что k-ая строка является линейной комбинацией первых r.
что означает, что k-ая строка является линейной комбинацией первых r. базисный минор имеет порядок < n
базисный минор имеет порядок < n 


