Задание №10. Определить изменение товарооборота в отчетном периоде по сравнению с базисным, если физический объем снизился на 20%
Определить изменение товарооборота в отчетном периоде по сравнению с базисным, если физический объем снизился на 20%, а цены возросли на 25%. Тема: Статистическое изучение связи социально-экономических явлений
Важнейшей задачей статистики является изучение взаимосвязей общественных явлений. Виды и формы этих взаимосвязей различны (рисунок А). Установление причинно-следственных связей между признаком-результатом (y) и признаком фактором (x) осуществляется с помощью различных статистических методов: - графического; - табличного или балансового; - сравнения параллельных рядов; - аналитических группировок; - дисперсионного анализа; - корреляционного анализа; - регрессионного анализа; - главных компонентов; - факторного анализа; - канонических корреляций; - многомерного гикалирования.
Рисунок А - Формы и виды взаимосвязей Исследование корреляционных связей в основном решает следующие задачи: 1)установление факта наличия (или отсутствия) взаимосвязи между признаками. Эта задача может решаться с помощью, так называемых, элементарных методов: графического, балансового, сравнения параллельных рядов, аналитических группировок и др.; 2)измерение тесноты связи между двумя (и более) признаками. Для решения этой задачи привлекается дисперсионный анализ, корреляционный анализ. Рассчитывается целый ряд коэффициентов, характеризующих тесноту связи: - коэффициент детерминации:
где
- эмпирическое корреляционное отношение:
- коэффициент линейной корреляции:
- индекс корреляции (для нелинейных взаимосвязей)
где yx – теоретические (выравненные) значения признака результата. - коэффициент корреляции рангов (коэффициент Спирмена):
где d –разность между рангами x и y по каждой единице совокупности; и другие; 3)определение математической модели зависимости признака-результата от признака-фактора, т.е. определение уравнения регрессии. Эта задача решается с помощью регрессионного анализа. Аналитическим выражением взаимосвязи может быть представлено: - уравнение прямой - уравнение параболы - уравнение гиперболы и т.д. Оценка параметров уравнений производится на основании метода наименьших квадратов. Так в случае линейной однофакторной взаимосвязи система нормальных уравнений для определения а0 и а1 имеет вид:
Экономическая интерпретация уравнения регрессии дается на основании коэффициента регрессии (а1) и коэффициента эластичности:
В современной статистике все большее распространение находят такие методы исследования взаимосвязей явлений, как метод главных компонент, метод факторного анализа, метод многомерного гикалирования и др., которые одновременно решают задачи и оценки тесноты связи и моделирования формы этой связи.
Контрольные вопросы:
1. Виды и формы взаимосвязей, изучаемых в статистике. 2. Назначение и сущность метода сравнения параллельных рядов. 3. Назначение и сущность метода аналитических группировок. 4. Назначение и сущность графического метода (корреляционного поля). 5. Назначение и сущность балансового метода (корреляционной таблицы). 6. Дисперсионный анализ. 7. Корреляционный анализ. 8. Регрессионный анализ. 9. Значение и роль индексного метода в изучении взаимосвязей. 10. Понятие о множественной корреляции. 11. Изучение взаимосвязи между качественным признаком.
|






 ,
, - межгрупповая дисперсия признака-результата;
- межгрупповая дисперсия признака-результата; - общая дисперсия признака результата.
- общая дисперсия признака результата.

 ,
, ,
, ,
,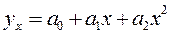 ,
,



 .
.


