Математическая модель задачи
Если зависимость уровня спроса от времени имеетлинейный характер, то функция, описывающая эту зависимость, имеет вид:
где
Если спрос не зависит от времени, то прогнозирующая функция имеет следующий вид:
Коэффициенты
где
Значение коэффициента
где
Для оценки степени точности прогноза необходимо вычислить стандартное отклонение фактических значений спроса от прогнозируемых. В статистическом анализе эта оценка называется среднеквадратическим отклонением и определяется по формуле
где
Для уравнения (1) Выбор лучшего прогноза осуществляется по минимальному значению Однако, следует иметь ввиду, что параметры уравнений регрессии рассчитаны на базе ограниченного объема статистики. Поэтому необходимо оценить тесноту связи между изучаемыми параметрами, т.е. степень влияния независимого фактора (
где
|

 (1)
(1) - прогнозируемое значение спроса в момент времени;
- прогнозируемое значение спроса в момент времени; - начальный и свободный коэффициент;
- начальный и свободный коэффициент; – коэффициент регрессии.
– коэффициент регрессии. . (2)
. (2)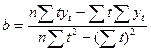 , (3)
, (3) - фактическое значение спроса, соответствующее моменту времени
- фактическое значение спроса, соответствующее моменту времени  ;
; - число периодов наблюдений;
- число периодов наблюдений; . (4)
. (4) , (5)
, (5) - арифметическое среднее фактического спроса.
- арифметическое среднее фактического спроса. , (6)
, (6) - число степеней свободы, связанное с количеством оцениваемых параметров в уравнении регрессии.
- число степеней свободы, связанное с количеством оцениваемых параметров в уравнении регрессии. .
. ). Для этого используем линейный коэффициент корреляции:
). Для этого используем линейный коэффициент корреляции: , (7)
, (7) - среднеквадратическое отклонение фактора
- среднеквадратическое отклонение фактора 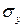 - среднеквадратическое отклонение фактора
- среднеквадратическое отклонение фактора 


