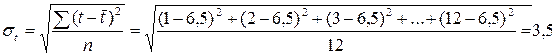Пример расчета. В таблице 5.1 приведены данные, характеризующие спрос за прошедшие 12 месяцев
В таблице 5.1 приведены данные, характеризующие спрос за прошедшие 12 месяцев. Требуется построить прогноз на следующий год и проанализировать результат. Таблица 5.1. Исходные данные
Рис. 1. График изменения уровня спроса
На графике виды колебания спроса в течение года. По этим данным построим два прогноза: 1) спроса, имеющего тенденцию к возрастанию при наличие случайных отклонений; 2) постоянного спроса со случайными отклонениями. Первый прогноз строится на основании уравнения (1), второй - уравнения (2). Для расчета коэффициентов регрессии по формулам (3), (4) и (5) составим вспомогательную таблицу 5.2.
Таблица 5.2.
Расчет параметров уравнения регрессии
Значение коэффициентов а и в для уравнения (1) равны:
Таким образом, уравнение регрессии имеет вид:
Прогноз уровня спроса на следующий год, составленный по этому уравнению регрессии, представлен в таблице 5.3.
Таблица 5.3
Прогностические оценки уровней спроса
Значение коэффициента а для выражения (2) равно 55,5( Оценим степень точности прогноза, полученного с помощью уравнения (1) и выражения (2), воспользовавшись формулой (6). Предварительно определим расчетные значения
Таблица 5.4.
Расчет стандартного отклонения
Если предположение о линейном характере поведения спроса верно, то уравнение (1) позволяет получить более точный прогноз, чем выражение (2). Стандартное отклонение, характеризующее погрешность прогноза, имеет меньшее значение. Если уровни спроса имеют нормальное распределение, то с вероятностью 0,68 можно утверждать, что в любой момент времени рассматриваемого периода уровни спроса будут лежать в интервале от 48 до 64 ед. ( Коэффициент корреляции определим по формуле (7):
Величина линейного коэффициента корреляции 0,73 говорит о том, что теснота связи между рассматриваемыми факторами достаточно велика и уравнение (1) может использоваться для прогнозирования спроса.
Приложение I
|



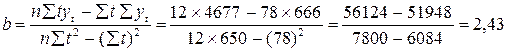


 ), Таким образом, прогностической оценкой спроса на следующий год является его средний уровень - 55,5. Для удобства вычислений примем
), Таким образом, прогностической оценкой спроса на следующий год является его средний уровень - 55,5. Для удобства вычислений примем  .
. за прошедший год.
за прошедший год.








 ). С вероятностью 0,95 можно утверждать, что уровень спроса окажется в интервале от 36 до 74 ед. (
). С вероятностью 0,95 можно утверждать, что уровень спроса окажется в интервале от 36 до 74 ед. ( ). И в интервале от 27 до 83 ед. (
). И в интервале от 27 до 83 ед. ( ). Эта вероятность составит 0,997.
). Эта вероятность составит 0,997.