Индивидуальные и сводные индексы
Индексы бывают: а) индивидуальные – характеризуют изменение элемента совокупности во времени и в пространстве, например: · индивидуальный индекс цены
где ·
 - -
где · индивидуальный индекс товарооборота
б) сводные – это сложные относительные показатели, которые характеризуют среднее изменение социально-экономических явлений, если они состоят из непосредственно несравниваемых элементов, например, сводный индекс товарооборота
Таким же образом можно рассчитывать сводный индекс цены
 : :
Между указанными индексами существует следующая связь:
Рассмотрим пример (табл. 3.1). Таблица 3.1 Реализации продукций А,В,С в регионе
Рассчитаем 1) 2) 3) Аналогичным образом можно рассчитывать индивидуальный индекс себестоимости
 : :
и сводный индекс производственных расходов
И наконец: Другим примером применения индексного метода является анализ изменения производительности труда. Имеются два подхода к выполнению расчета: а) учет выработанной продукции за единицу времени б) определение рабочего времени Эти две величины взаимосвязаны: В этом случае индивидуальный индекс производительности труда равен:
где Сводный индекс производительности труда –
а сводный индекс трудового времени –
Здесь также
|


 (3.1)
(3.1) и
и  - цены на товар в текущем и базисном периодах;
- цены на товар в текущем и базисном периодах;
 и
и  - объемы реализации товара в текущем и базисном периодах;
- объемы реализации товара в текущем и базисном периодах;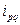 -
- ; (3.3)
; (3.3) -
- (3.4)
(3.4)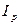 :
:
 .
.
 , драм
, драм
 , кг
, кг
 , драм
, драм
 , кг
, кг
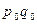
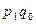

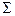
 :
: т.е. цены во II квартале упали на 10,8%;
т.е. цены во II квартале упали на 10,8%; физический объем реализации увеличился на 8,6%;
физический объем реализации увеличился на 8,6%; несмотря на положительные изменения индексов
несмотря на положительные изменения индексов 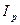 и
и 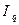 , товарооборот во II квартале упал на 3,1 %
, товарооборот во II квартале упал на 3,1 % :
: 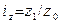 ,
,
 :
: . (3.7)
. (3.7) (3.8)
(3.8) ;
; , расходованного для получения единицы продукции.
, расходованного для получения единицы продукции. .
. или
или  , (3.9)
, (3.9)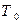 ,
,  - суммарный расход времени, затраченный для получения продукции в текущем и базисном периодах.
- суммарный расход времени, затраченный для получения продукции в текущем и базисном периодах. , (3.10)
, (3.10) . (3.11)
. (3.11) или
или  . (3.12)
. (3.12)


