Характеристики основных тенденций развития
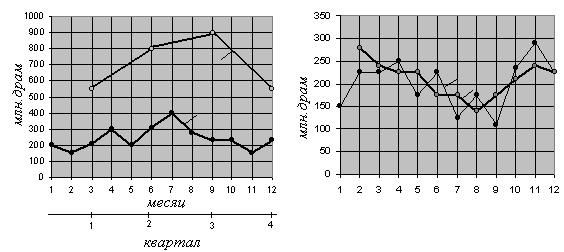
Уровни рядов динамики формируются в результате интегрального воздействия кратковременных и длительно действующих факторов, которые в большинстве случаев носят случайный характер. Выявление закономерностей изменения рядов динамики подразумевает компенсацию случайной составляющей факторов. Поэтому для выявления основных тенденций развития необходимо выравнивать уровни рядов динамики, что позволяет полнее характеризовать изменение рядов динамики и представить этот ряд как временную функцию основных тенденций развития (тренд). Рассмотрим методы выявления тренда. 1. Укрупнение интервалов рядов динамики – предварительный ряд преобразуется и заменяется другим, с более крупным временным интервалом, например, месячное изменение рассматриваемого экономического показателя (рис. 2.3, график1)представляется квартальными (рис. 2.3, график 2) или полугодовыми интервалами.
3. Аналитический метод выравнивания ряда динамики – в этом случае, учитывая общий характер изменения уровней динамики, выбирается аналитическая функция, которая наиболее подходит указанному изменению. Эта функция называется трендовой математической моделью. Выбор подходящей аналитической функции основывается на анализе уровней ряда или априопорной информации изменения тренда. Втабл. 2.1 представлены наиболее часто применяемые трендовые функции. Таблица 2.1 Виды трендовых функций
На рис. 2.5 дан пример замены уровней ряда трендовой функцией.

Рис.2.5. Аналитический метод выравнивания 4. Метод конечных разностей. Представим, что уравнение тренда является прямой линией
По результатам расчетов получим:

Если тренд представляется параболой 2-ого порядка:
то постоянными являются вторые разности: нулевыми – третье разности: Тогда:
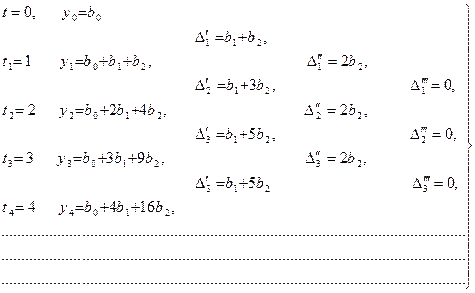
5. Применение метода корреляционного анализа. Часто становится необходимым выявление степени взаимосвязи между исследуемыми экономическими явлениями, протекающими во времени, которые можно реализовать применением метода корреляционного анализа. Для рядов динамики при этом можно решить следующие задачи: а) установление связи между уровнями и периодами ряда; б) аналитическое выравнивание ряда и получение его математической модели. Из всего разнообразия связей рассмотрим случай, когда между нормально распределенными переменными
где Статистические параметры, входящие в (2.15), рассчитываются следующим образом: а) средние значения – б) среднеквадратические отклонения – в) коэффициент корреляции – Если

Таблица 2.2 Расчет параметров уравнения (2.15)
6. Выравнивание данных применением метода наименьших квадратов (МНК). Аналитический метод выравнивания рядов динамики обычно выполняется в два этапа: а) выбор вида трендовой функции, исходя из предварительного графического анализа рядов динамики или при наличии априорной информации о виде этой функции; б) определение параметров выбранного вида трендовой функции методом наименьших квадратов (МНК).
· линейная –
 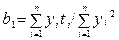 ; ;
· параболическая, 2-го порядка – где значения

· гиперболическая –
где значения
7. Получение уравнения тренда с помощью преобразования рядов Фурье (для сезонных неравномерностей).
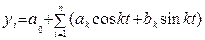 , ,
где гармоника ряда берется в пределах Используя метод наименьших квадратов, в этом случае получаем:
   . .
Обычно расчеты ведутся для одного года, т.е.
|









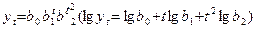

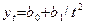
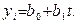 Примем, что постоянными являются первые разности:
Примем, что постоянными являются первые разности:  и нулевыми – вторые разности:
и нулевыми – вторые разности:  .
.
 ,
,
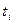 и
и 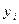 существует линейная корреляционная связь. Уравнение регрессии при этом выражается следующим образом:
существует линейная корреляционная связь. Уравнение регрессии при этом выражается следующим образом: (2.15)
(2.15) – параметр линии регрессии;
– параметр линии регрессии;  – коэффициент регрессии.
– коэффициент регрессии.
 ; (2.16)
; (2.16) ,
,  ; (2.17)
; (2.17) где
где  . (2.1Если
. (2.1Если  , можно судить о наличии прямолинейной связи между рассматриваемыми значениями
, можно судить о наличии прямолинейной связи между рассматриваемыми значениями  и
и  –прямолинейная связь достаточно высокая.
–прямолинейная связь достаточно высокая. , функция убывающая, а если
, функция убывающая, а если 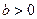 – возрастающая. Для определения статистических параметров уравнения (2.15) составляют двумерную корреляционную таблицу, предварительно создав вариационный ряд значении
– возрастающая. Для определения статистических параметров уравнения (2.15) составляют двумерную корреляционную таблицу, предварительно создав вариационный ряд значении 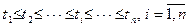 , где n – число точек
, где n – число точек  . (2.19)
. (2.19)




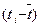


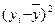




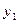






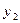





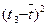

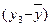



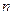
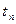

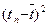








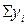
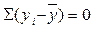




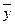


 ,
,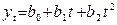 ,
, ,
,  и
и  определяются из системы уравнений:
определяются из системы уравнений: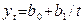 ,
, определяются из системы уравнений
определяются из системы уравнений
 При анализе сезонных неравномерностей трендовую функцию целесообразно получить, используя преобразование Фурье:
При анализе сезонных неравномерностей трендовую функцию целесообразно получить, используя преобразование Фурье: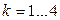 .
. .
.


