Классическая линейная модель множественной регрессииDeparture
Summer Camp with EFL School!
Дорогие родители! Ваш ребенок остаётся летом в городе? Некому за ним присмотреть? Боитесь, что без присмотра он будет «общаться» только с телевизором и компьютером? Выход есть — запишите его в наш летний языковой лагерь! Это городской лагерь для детей до 12 лет с любым уровнем владения языком. Здесь можно интересно и познавательно провести время, а также найти новых друзей.
Лагерь 2014 будет работать со 2 по 27 ИЮНЯ!!! В программу лагеря входят следующие мероприятия: - зарядка по утрам (детская йога); - занятия английским языком по 2-3 часа в день; - полноценный обед и полдник; - прогулки, подвижные игры; - развлекательная программа: театральные постановки, песни, игры, просмотр фильмов и мультиков и многое другое (на английском языке); - культурная и экскурсионная программы; - занятия творчеством, hand-made.
Количество мест ограничено! Спешите подарить вашим детям замечательный и полезный отдых! Наш адрес: Щетинина, 7.
Подробности и раннее бронирование по тел.: 501-655; 8911-501-16-55 Group quotation
PLEASE UNDERSTAND! THIS IS ENGLISH EMERSION COURSE THUS THERE IS NO RUSSIAN LANGUAGE WILL BE ALLOWED!! WE WILL SPEAK ONLY IN ENGLISH!!! Academic programme · Summer Plus course: 25 lessons/week · Minimum 18 years of age · Maximum 12 students per class in closed groups · Course materials · Timetable: Mornings 0900 - 1030, 1100 - 1230, afternoons 1330-1445 (no lessons Weds & Fri pm) · Certificate of attendance at the end of the course Social programme · Afternoon programme: 2 afternoon activities and a half day excursion per week · Evening programme: free events at the school, events at cost outside school. Minimum 2 evening events per week (disco, karaoke, student night) · Weekend: full day excursion to London on Saturday or Sunday Accommodation · Friendly homestay within walking distance to the school (no more than 30 minutes). · Sharing room with a member of the same group. · Breakfast and evening meals, with lunch at weekends. (Lunch not included on weekdays, packed lunches/meal vouchers can be arranged) Airport Transfers · Transfer shuttle London Heathrow from and to host family in Eastbourne on arrival/departure
RCW/ 29.04.2013 ВЫБОРОЧНОЕ СОДЕРЖАНИЕ ТЕСТОВЫХ МАТЕРИАЛОВ Классическая линейная модель множественной регрессии 1. Задание {{ 8 }} КЛММР1 Дана ковариационная матрица вектора
Оценка дисперсии элемента b 2 вектора b равна …
2. Задание {{ 9 }} КЛММР2 Дана ковариационная матрица вектора
Оценка дисперсии элемента b 1 вектора b равна …
3. Задание {{ 10 }} КЛММР3 Дана ковариационная матрица вектора
Оценка дисперсии элемента b 0 вектора b равна …
4. Задание {{ 11 }} КЛММР5 При исследовании зависимости себестоимости продукции y от объема выпуска x 1 и производительности труда x 2 по данным n = 20 предприятий получено уравнение регрессии
5. Задание {{ 12 }} КЛММР6 При исследовании зависимости себестоимости продукции y от объема выпуска x 1 и производительности труда x 2 по данным n = 20 предприятий получено уравнение регрессии
6. Задание {{ 13 }} КЛММР7 При исследовании зависимости себестоимости продукции y от объема выпуска x 1 и производительности труда x 2 по данным n = 20 предприятий получено уравнение регрессии
7. Задание {{ 14 }} КЛММР8 Уравнению регрессии
8. Задание {{ 20 }} КЛММР11 Для оценки мультиколлинеарности факторов используется... 9. Задание {{ 23 }} КЛММР9 Чем ближе к 1 определитель матрицы межфакторной корреляции, тем... 10. Задание {{ 24 }} КЛММР10 Чем ближе к 0 определитель матрицы межфакторной корреляции, тем... 11. Задание {{ 170 }} КЛММР35 Выполните анализ следующей матрицы парных коэффициентов корреляции и сделайте вывод о наличии мультиколлинеарности....
12. Задание {{ 54 }} КЛММР14 В случае множественной регрессии тесноту совместного влияния факторов на результат оценивает... 13. Задание {{ 60 }} КЛММР13 Дисперсия остатков модели должна быть постоянной для всех наблюдений. Это условие... 14. Задание {{ 62 }} КЛММР12 Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы... 15. Задание {{ 69 }} КЛММР15 Долю дисперсии, объясняемую регрессией, в общей дисперсии эндогенной переменной y характеризует... 16. Задание {{ 72 }} КЛММР16 Если условия Гаусса-Маркова для остаточного члена выполнены, то коэффициенты регрессии, построенные простым МНК, будут... 17. Задание {{ 77 }} КЛММР18 Тесная линейная зависимость между факторами при построении уравнения множественной регрессии представляет собой проблему... 18. Задание {{ 113 }} КЛММР4 При исследовании зависимости себестоимости продукции y от объема выпуска
19. Задание {{ 114 }} КЛММР17 При исследовании зависимости себестоимости продукции y от объема выпуска
20. Задание {{ 116 }} КЛММР19 Уравнению регрессии 21. Задание {{ 117 }} КЛММР20 По данным
22. Задание {{ 118 }} КЛММР21 По данным
23. Задание {{ 119 }} КЛММР22 По данным
24. Задание {{ 120 }} КЛММР23 По данным
25. Задание {{ 123 }} КЛММР24 Коэффициент детерминации равен отношению вариаций... 26. Задание {{ 124 }} КЛММР25 Остаточная вариация эндогенной переменной это... 27. Задание {{ 125 }} КЛММР26 Воспроизведенная вариация эндогенной переменной это... 28. Задание {{ 126 }} КЛММР27 Для сравнения экзогенных факторов по степени их влияния на эндогенную переменную используются... 29. Задание {{ 140 }} КЛММР28 Значение коэффициента детерминации рассчитывается как отношение дисперсии результативного признака, объясненной регрессией, к __________ дисперсии результативного признака 30. Задание {{ 142 }} КЛММР29 С помощью частного F-критерия можно проверить значимость j-го коэффициента чистой регрессии в предложении, что j-й фактор в уравнение множественной регрессии... 31. Задание {{ 143 }} КЛММР30 Если оценки параметров уравнения регрессии, полученных при помощи метода наименьших квадратов обладают свойствами несмещенности, эффективности и состоятельности, то... 32. Задание {{ 146 }} КЛММР31 Одним из современных препятствий эффективного применения множественного регрессионного анализа является...
|
Based on 10-12 students and 1 group leader
.
и среднеквадратичные отклонения коэффициентов регрессии 
и 
. На уровне значимости a = 0,05 можно утверждать, что …
. C доверительной вероятностью g = 0,95 средняя себестоимость продукции при увеличении объема производства x 1 на единицу может максимально измениться на …
, 
, 
. Если производительность труда x 2 увеличить на 1%, то себестоимость продукции в среднем изменится на…
. Доля вариации (в %) переменной y объясненная переменными x 1 и x 2 равна…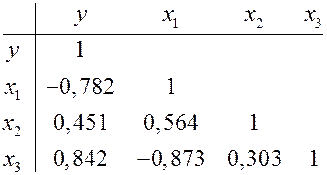
и производительности труда 
по данным 
предприятий получено уравнение регрессии 
можно утверждать, что в уравнении регрессии…
, при уменьшении объема производства 
. Переменными 
фирм исследована зависимость прибыли y от числа работающих x вида 
. Была получена оценка остаточной дисперсии 
и обратная матрица 
. Дисперсия оценки коэффициента регрессии 
равна…
регионов получена регрессионная модель объема реализации медикаментов на одного жителя y в зависимости от доли городского населения 
и среднеквадратичные отклонения коэффициентов регрессии 
и 
. Можно утверждать, что y зависит от доли городского населения 
верхняя граница интервальной оценки коэффициента регрессии при 
