Ряд Тейлора
Теорема. (О разложении функции в степенной ряд). Если функция f (x) может быть разложена в сходящийся к ней степенной ряд (13.3.9)
то это разложение единственно и коэффициенты степенного ряда в этом случае определяются формулами: a 0 = f (x0), a 1 = f ¢(x 0), Доказательство. Пусть
При х = х 0 следует что f (x 0) = a0. Последовательно дифференцируя равенство (13.3.10) получим f ¢(x) = a 1 + 2 a 2 (x – x 0) +… f ¢¢(x) = 2 a 2 + 2∙3∙ a 3 (x – x 0) +… f ¢¢¢(x) = 2∙3∙ a 3 +… ………….. f (n)(x) = n! an + … …………… Положив в полученных равенствах х = х 0 найдём: f ¢(x 0) = a 1. f ¢¢(x 0) = 2 a 2. Þ f ¢¢¢(x 0) = 2∙3∙ a 3 Þ ……………………………. f ( n )(x0) = n! an Þ ……………………………… Таким образом, мы получили, что все коэффициенты а 0, а 1, а 2, ¼, ап, ¼, определяются единственным образом формулами:
a 0 = f (x 0), a 1 = f ¢(x 0), …, что и доказывает теорему. Подставляя найденные выражения в ряд (13.3.10) получим ряд f (x)= f (x 0) + f ¢(x 0) (х – х 0)+
Определение. Рядом Тейлора функции f (x) в окрестности точки х 0 называется степенной ряд f (x 0) + f ¢(x 0) (х – х 0)+ относительно разности (х – х 0), а его коэффициенты ряда называются коэффициентами Тейлора функции f (x) в точке х 0. Таким образом, мы установили, что если функцию f (x) можно разложить в степенной ряд по степеням (х – х 0), то этот ряд обязательно является рядом Тейлора этой функции. Обратим внимание на тот факт, что все рассуждения были сделаны в предположении, что f (x) может быть разложена в степенной ряд. Поставим теперь вопрос о том, когда заданную функцию можно разложить в степенной ряд. Как указано выше, необходимым условием для возможности такого разложения является дифференцируемость функции f (x) бесконечное число раз.. В дальнейшем станет ясно, что это условие не является достаточным. Определение. Если в ряде (13.3.12) х 0 = 0, то полученный ряд называется рядом Маклорена, т.е. f (x)= f (0) + f ¢(0) х + Определение. Многочлен Определение. Величина Rn (x) = f (x) – Sn (x) (13.3.14) называется п - м остаточным членом ряда Тейлора функции f (x) в точке х 0. Теорема. (Условие разложимости функции в ряд Тейлора). Для того, чтобы ряд Тейлора сходился на интервале (x 0- R; x 0+ R) и имел своей суммой функцию f (x) необходимо и достаточно, чтобы на этом интервале остаточный член Rn (x) ряда Тейлора стремился к нулю при п → ¥, т. е. Из теоремы вытекает, что вопрос о разложимости функции в ряд Тейлора сводится к исследованию поведения остаточного члена Rn (x) при п → ¥. То есть, если для какой-либо функции формально написан ряд Тейлора, то для того, чтобыдоказать, что ряд представляет функцию необходимо или доказать, что остаточный член Rn (x)→0 при п → ¥, или каким-либо иным способом удостовериться, что ряд сходится к функции. Для каждой каждой элементарной функции существует такое x 0 и такое R, что в интервале (x 0- R; x 0+ R) она разлагается в ряд Тейлора или (при x 0 = 0) в ряд Маклорена.
|

 , ………(13.3.10)
, ………(13.3.10) , …,
, …, 

 ;
;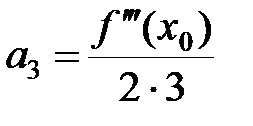
 +…+
+…+  +… (13.3.11)
+… (13.3.11) + …+
+ …+  + … (13.3.13)
+ … (13.3.13) называется многочленом Тейлора п - й степени функции f (x) по степеням (х – х 0).
называется многочленом Тейлора п - й степени функции f (x) по степеням (х – х 0). для
для  х
х  (x 0- R; x 0+ R).
(x 0- R; x 0+ R).


