Теорема Абеля.
1) Если степенной ряд (13.3.1) сходится при х = х 0 (х 0¹0), то он сходится, и притом абсолютно, для любых х удовлетворяющих условию | х |<| x 0|; 2) Если ряд (1) расходится при х = х 1, то он расходится для любых х, удовлетворяющих условию | х |>| x 1|. Доказательство. 1) Так как по условию числовой ряд
Перепишем ряд (13.3.1) в виде
и рассмотрим ряд, составленный из абсолютных величин его членов
Члены ряда (13.3.3), в силу неравенства (13.3.2) меньше соответствующих членов ряда
При | х |<| x 0| ряд (13.3.4) представляет собой геометрическую прогрессию со знаменателем 2) По условию, в точке х 1 ряд (1) расходится. Докажем, что он расходится для любого х: | х |>| x 1|. Предположим обратное, т. е. допустим, что при некотором значении х, таком, что | х |>| x 1|, ряд (13.3.1) сходится. Тогда по только что доказанной первой части теоремы этот ряд должен сходится в точке х 1, т. к. | x 1|<| х |. Но это противоречит условию теоремы. Теорема доказана. Следствие. Если ряд (13.3.1) сходится не при всех значениях х и не только в точке х =0, то существует число R >0 такое, что ряд абсолютно сходится при | х |< R и расходится при | х |> R. (без доказательства). Определение. Радиусом сходимости степенного ряда называется такое число R, что для всех х: | х |< R, степенной ряд сходится, а для любого х: | х |> R, расходится. Интервал (-R; R) называется интервалом сходимости. Множество точек, в которых ряд сходится, называется областью сходимости степенного ряда. Область сходимости есть интервал сходимости, который может включать один или оба его конца. Замечание. 1) Если R =0, то ряд сходится в единственной точке х =0. Если R =¥, то ряд сходится при всех х. 2) При х = ± R ряд может, как сходится, так и расходится. Вопрос о сходимости ряда решается индивидуально для каждого конкретного ряда
Теорема (о способе определения радиуса сходимости). Если существует
то радиус сходимости ряда (13.3.1) равен
Доказательство. Исследуем ряд (13.3.1) на сходимость по признаку Даламбера. По условию теоремы существует предел (13.3.5). Обозначим его
При каждом значении х ряд становится числовым. Поэтому по признаку Даламбера ряд При | х |> R этот ряд расходится, т. к.
и его общий член интервала (-R; R) и расходится вне его, при этом Замечание. Аналогичным образом, для определения интервала сходимости можно пользоваться радикальным признаком сходимости Коши. Тогда радиус сходимости ряда (1) определяется формулой
если предел, стоящий в знаменателе существует.
|

 сходится, то его общий член
сходится, то его общий член  → 0при п →∞. Отсюда следует, что существует число М >0 такое, что все члены ряда по абсолютной величине меньше М,т.е.
→ 0при п →∞. Отсюда следует, что существует число М >0 такое, что все члены ряда по абсолютной величине меньше М,т.е. . (13.3.2)
. (13.3.2)
 (13.3.3)
(13.3.3)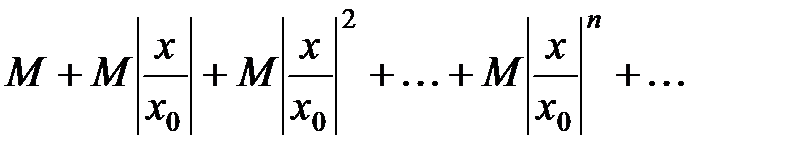 (13.3.4)
(13.3.4) и, следовательно, сходится. Так как члены ряда (13.3.3) меньше соответствующих членов ряда (13.3.4), то, по признаку сравнения, ряд (13.3.3) также сходится, а это значит, что ряд (13.3.1) сходится абсолютно.
и, следовательно, сходится. Так как члены ряда (13.3.3) меньше соответствующих членов ряда (13.3.4), то, по признаку сравнения, ряд (13.3.3) также сходится, а это значит, что ряд (13.3.1) сходится абсолютно.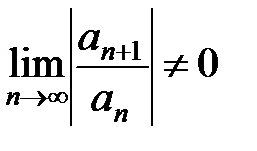 , (13.3.5)
, (13.3.5) . (13.3.6)
. (13.3.6) . Тогда
. Тогда
 .
. сходится, если
сходится, если  , т. е. | х |< R. Следовательно, по достаточному признаку сходимости знакопеременного ряда ряд (13.3.1) сходится абсолютно при | х |< R.
, т. е. | х |< R. Следовательно, по достаточному признаку сходимости знакопеременного ряда ряд (13.3.1) сходится абсолютно при | х |< R.
 при п ®∞. Таким образом ряд сходится внутри
при п ®∞. Таким образом ряд сходится внутри , (13.3.7)
, (13.3.7)


