Вычисление определенных интегралов с помощью рядов
Степенные ряды имеют разнообразные приложения. С их помощью с любой заданной точностью вычисляют значения функций (в частности значения π и e). Значительную роль играют степенные ряды в приближенных методах решений дифференциальных уравнений. Определенные интегралы от различных типов функций за малым исключением не вычисляются по формуле Ньютона – Лейбница, например,
С помощью рядов находят приближенные значения таких определенных интегралов, которые или не выражаются через элементарные функции или сложны для вычислений. Среди них часто встречающиеся в практических приложениях математики. Рассмотрим несколько примеров. 1. Пусть требуется вычислить интеграл Здесь первообразная от вычисления этого интеграла разложим подынтегральную функцию в ряд
заменяя в разложении
Интегрируя обе части этого равенства в пределах от 0 до a, получим
С помощью этого равенства мы можем при любом a вычислить данный интеграл с любой степенью точности. 2. Пусть требуется вычислить интеграл Из равенства
получаем
последний ряд сходится при всех значениях x. Интегрируя почленно, получим
Сумма ряда вычисляется с любой заданной степенью точности при всех a.
Сводная таблица основных формул по теме «Функциональные ряды»
|
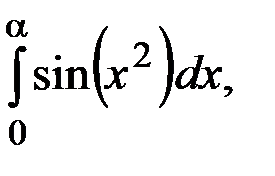
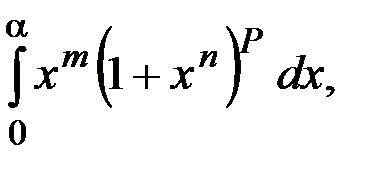
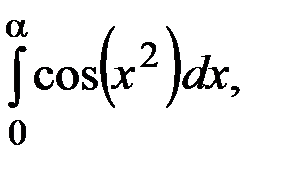
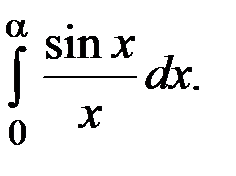и др.
.
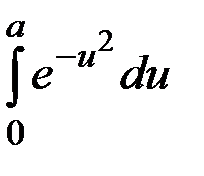не является элементарной функцией. Для
,тогда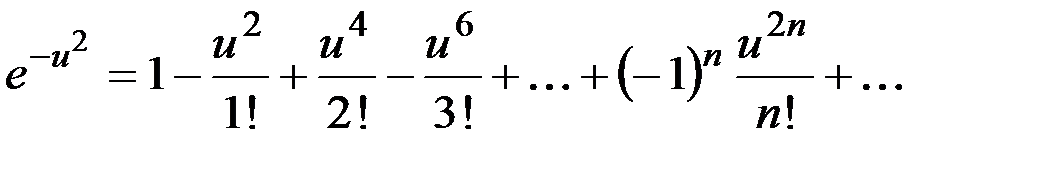
.
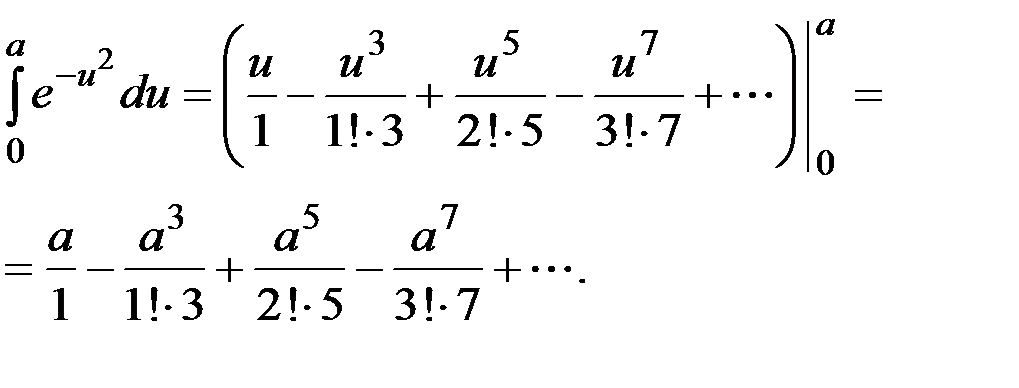
Этот интеграл не берется в элементарных функциях, поскольку первообразная функции 
не является элементарной. В то же время эта первообразная легко выражается в виде степенного ряда.
,
.
,
где u 1, u 2,…, u n,…- функции переменной х.
х 0 = 0, 
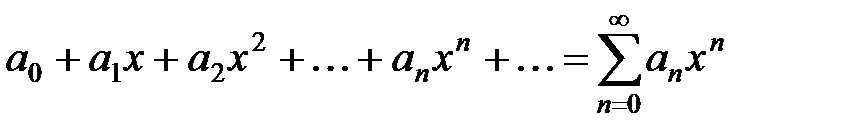
По радикальному признаку Коши
+ …+ 
+ …
+ …+ 
+ …
