ПРИМЕРЫ РЕШЕНИЯПРАКТИЧЕСКИХ ЗАДАЧ
Пример 1. Найти область сходимости степенного ряда Решение. Интервал сходимости ряда (–5; 5). Исследуем сходимость ряда на концах интервала сходимости. При Пример 2. Определить интервал сходимости ряда
Решение. Применяя признак сходимости Даламбера, получим
Так как предел не зависит от x и меньше единицы, то значит ряд сходится при всех значениях x. Пример 3. Определить интервал сходимости ряда
Решение. Этот ряд расходится при всех значениях x, кроме
Пример 4. Определить интервал сходимости ряда Решение. Здесь
Следовательно, данный ряд сходится на интервале (–1; 1). Исследуем поведение ряда на концах интервала сходимости, то есть в точках При x = 1 получаем гармонический ряд При x = –1 получаем ряд
Пример 5. Разложить в ряд по степеням х функцию Воспользуемся разложением Полагаем
Отсюда
Пример 6. Разложить в ряд по степеням х функцию Запишем Положим
или
Пример 7. Разложить функцию Воспользуемся разложением функции f (x) в ряд Тейлора
В последней формуле примем х0 = π / 2. Последовательно Дифференцируя, найдём:
и т.д., таким образом
Пример 8 Вычислить определенный интеграл Решение. Разложим подынтегральную функцию в степенной ряд. Воспользуемся уже известным рядом: . Заменив в нем x на . Умножим обе части равенства на отсюда
Замечаем, что третий член ряда по абсолютной величине меньше 0,001. Следовательно, для решения данной задачи, согласно признаку Лейбница, надо взять сумму первых двух членов, что обеспечит требуемую точность:
|
.
. Найдем радиус сходимости ряда по формуле (4): 
.
получим ряд 
, который сходится по признаку Лейбница. При 
получим ряд 
, который сходится (это ряд Дирихле). Область сходимости данного ряда 
.
.
.
.
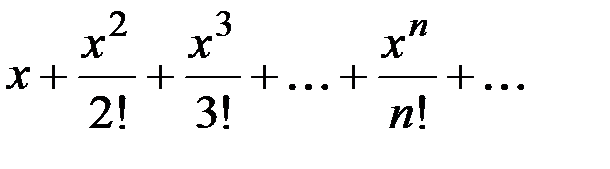, так как 
при 
, каково бы ни было x, отличное от 0.
.
. Поэтому
.
.
(он расходится).
. Он сходится в силу признака Лейбница. Данный ряд сходится в любой точке полуинтервала 
и расходится вне его.
.
и получим
.
.
.
и воспользуемся разложением 
, 
. Тогда
в ряд по степеням 
; 
;
; 
;
; 
;
; 
;
; 
;
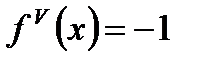с точностью
, получим 
: 
,
.
