Свойства степенных рядов.
Определение. Пусть функция f (x) является суммой степенного ряда
интервал сходимости которого (-R; R). В этом случае говорят, что на (-R; R) f (x) разлагается в степенной ряд или ряд по степеням х. Теорема 1. Если функция f (x) на интервале (-R; R) разлагается в степенной ряд (13.3.8), то она дифференцируема на этом интервале и ее производная f¢;(x) может быть найдена почленным дифференцированием членов этого ряда, т. е.
f¢;(x)= а 1+2 а 2 х +3 а 3 х 2+¼+ папхп- 1+¼
Аналогично могут быть вычислены производные любого порядка функции f (x). При этом соответствующие ряды имеют тот же радиус сходимости, что и ряд (13.3.8). Теорема 2. Если функция на f (x) на интервале (-R; R) разлагается в степенной ряд (13.3.8), то она интегрируема на (-R; R) и интеграл от нее может быть вычислен почленным интегрированием ряда (13.3.8), т. е. если а, b Î(-R; R), то
При этом полученный степенной ряд имеет тот же радиус сходимости, что и ряд (13.3.8). Замечание. Иногда рассматривают степенной ряд более общего вида:
Если f (x)-сумма ряда, то говорят, что f (x) разлагается в сходящийся к ней степенной ряд по степеням х - х 0. Все сказанное выше остается в силе для ряда (13.3.9), с той разницей, что центр интервала сходимости будет лежать не в точке х =0, а в точке х = х 0.
Областью сходимости степенного ряда(13.3.9) является интервал (x 0- R; x 0+ R), к которому могут присоединиться один или оба его конца.
|
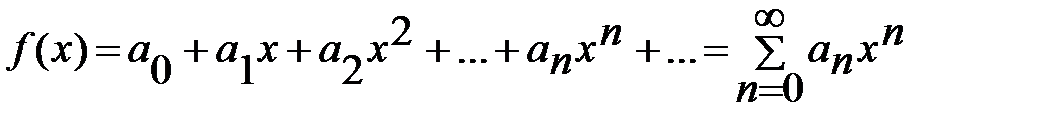, (13.3.8)
.
. (13.3.9)
