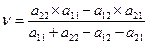Метод теории игр при принятии решений в условиях неопределенности

При принятии решений в условиях неопределенности очень широко используется метод теории игр. Теория игр – это математическая теория конфликтных ситуаций. Задача этой теоpии – выработка рекомендаций по рациональному образу действий участников конфликта. При этом строят упрошенную модель конфликтной ситуации, называемую игрой. Под «игрой» понимают мероприятие, состоящее из ряда действий или «ходов». От реальной конфликтной ситуации игра отличается тем, что ведется по вполне определенным правилам. Сторо­ны, участвующие в конфликте, называют игроками, исход конфликта - выигрышем и т.д.

Если в игре сталкиваются интересы двух сторон, то игра называется парной, если сторон больше - множествен­ной. Множественная игра с двумя постоянными коалициями обращает игру в парную. Наибольшее практическое значе­ние имеют парные игры. Рассматрим конечную игру, в которой игрок А имеет m стратегий, а игрок В - n стратегий. Та­кая игра называется m x n. Стратегии, соответственно, обозначим: А₁, А₂,..., А_m - для игрока А; В₁, В₂,..., В_n - для игрока В. Если игра состоит только из личных ходов, то выбор стратегий А_i и В_j игроками однозначно определяет исход игры - наш выигрыш a_ij Если известны a_ij для всех сочетаний стратегий, то они образуют платежную матрицу размером m x п, где: m - число строк матрицы, а n - число его столбцов.

Принцип осторожности, диктующий игрокам выбор соответствующих стратегий (максиминной и минимаксной), является в теории игр основным принципом и называется принципом минимакса. В платежной матрице такой игры существует элемент, являющийся одновременно минимальным в своей строке и максимальным в своем столбце. Такой элемент назы­вают седловой тонкой. При этом значение v=ą=þ назы­вают чистой ценой игры. В этом случае решение игры (совокупность оптимальных стратегий игроков) обладает следующим свойством: если один из игроков придерживает­ся своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной страте­гии [2]. Если верхняя цена игры не совпадает с нижней, то в этом случае стоит говорить об игре в смешанных стратегиях. Смешанной S_A называется применение чистых стратегий А₁,А₂,…,А_n с вероятностью p₁,p₂,…,p_n, а смешанной стратегией S_B - применение чистых стратегий B₁,B₂,…,B_n с вероятностью p₁,p₂,…,p_m. Пусть игра имеет размерность 2 на 2 и задается платежной матрицей:

Для игрока А оптимальная стратегия будет иметь вероятности:

; ; цена игры