Критерии принятия решения в условиях риска
При принятии решений в условиях риска необходимо воспользоваться инструментом, который называется ожидаемая ценность. Он фокусируется на оценке, количественном измерении и графическом изображении масштабов и природы риска. Ожидаемая ценность – это произведение величины вероятности и суммы выплаты (суммы приза). Это можно показать на графике как площадь прямоугольника, где основание – размер выплаты (размер приза), а высота – вероятность выигрыша (с размерностью от нуля до единицы, 0 – это отсутствие шанса, 1 – полная достоверность) Ожидаемая ценность решения – сумма индивидуальных ожидаемых ценностей для каждого результата. Принятие решений в условиях риска может быть основано на следующих критериях: — критерий ожидаемого значения; — комбинация ожидаемого значения и дисперсии; — известного предельного уровня; — наиболее вероятного события в будущем. 1.Критерий ожидаемого значения (КОЗ) Использование данного критерия предполагает принятие решения, обуславливающего максимальную прибыль при имеющихся исходных данных о вероятности полученного результата при том или другом решении. Критерий ожидаемого значения представляет собой выбранные средние значения случайной величины. Достоверность получаемого решения будет зависеть от объема выборки. Если через 2. Критерий «ожидаемого значения – дисперсия» Недостаток критерия ожидаемого значения устраняется применением комбинации его и выборочной дисперсии. Возможным критерием при этом является минимум выражения: 3. Критерий предельного уровня Этот критерий не имеет четко выраженной математической формулировки и основан в значительной степени на интуиции и опыте лица принимающего решение, которое на основании субъективных соображений определяет наиболее приемлемый способ действий. Критерий предельного уровня обычно не используется, когда нет полного представления о множестве возможных альтернатив. Учет ситуации риска при этом может производиться за счет введения законов распределений случайных факторов для известных альтернатив. Несмотря на отсутствие формализации, критерием предельного уровня пользуются довольно часто, задавая их значения на основании экспертных или опытных данных. 4. Критерий наиболее вероятного исхода Этот критерий предполагает замену случайной ситуации детерминированной путем замены случайной величины прибыли (или затрат) единственным значением, имеющим наибольшую вероятность реализации. Использование данного критерия, также как и в предыдущем случае в значительной степени опирается на опыт и интуицию. При этом необходимо учитывать два обстоятельства, затрудняющие применение этого критерия: — критерий нельзя использовать, если наибольшая вероятность — применение критерия невозможно, если несколько значений Случай, когда неопределенные факторы заданы распределением, соответствует ситуации риска. Этот случай может учитываться двумя путями. Первый - анализом адаптивных возможностей, позволяющих реагировать на конкретные исходы; второй - методически, при сопоставлении эффективности технических решений. Суть первого подхода заключается в том, что законы распределения отдельных параметров на этапе проектирования могут быть определены с достаточной степенью приближения на основе сопоставления с аналогами, из физических соображений или на базе статистических данных и данных прогнозов. Методический учет случайных факторов, заданных распределением, может быть выполнен двумя приемами: заменой случайных параметров их математическими ожиданиями (сведением стохастической задачи к детерминированной) и «взвешиванием» показателя качества по вероятности (этот прием иногда называют «оптимизация в среднем»). При описании дискретных случайных величин наиболее часто используют распределения Пуассона (биноминальное). Для непрерывных величин основными распределениями являются нормальное, равномерное и экспоненциальное распределения.
|

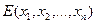 обозначить критерий ожидаемого значения, где
обозначить критерий ожидаемого значения, где 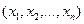 - принимаемые решения при их количестве, равным n, то
- принимаемые решения при их количестве, равным n, то 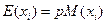 , где
, где 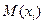 - математическое ожидание критерия. Делаем вывод, критерий ожидаемого значения можно применять, когда однотипные решения в сходных ситуациях приходится принимать большое число раз.
- математическое ожидание критерия. Делаем вывод, критерий ожидаемого значения можно применять, когда однотипные решения в сходных ситуациях приходится принимать большое число раз.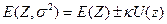 , где
, где 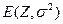 - критерий «ожидаемого значения – дисперсия»,
- критерий «ожидаемого значения – дисперсия», 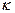 - постоянный коэффициент,
- постоянный коэффициент, 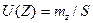 - выборочный коэффициент вариации,
- выборочный коэффициент вариации, 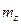 - оценка математического ожидания, S – оценка среднего квадратического ожидания. Знак «минус» ставится в случае оценки прибыли, знак «плюс» - в случае затрат. С использованием данного критерия точность предсказания повышается за счет учета возможного разброса значений E(Z).
- оценка математического ожидания, S – оценка среднего квадратического ожидания. Знак «минус» ставится в случае оценки прибыли, знак «плюс» - в случае затрат. С использованием данного критерия точность предсказания повышается за счет учета возможного разброса значений E(Z).


