Свободное падение и его ускорение
В природе существует естественное равноускоренное движение — это свободное падение. Свободным падением называется падение тела, если на него действует единственная сила — сила тяжести. Опыты, проведенные Галилеем, показали, что при свободном падении все тела движутся с одинаковым ускорением, которое называют ускорением свободного падения и обозначают буквой g. Вблизи поверхности Земли g На рис. 3.16 приведены стробоскопические фотографии стального шарика, падающего вертикально вниз без начальной скорости, и шарика, которому сообщена горизонтальная скорость.
Рис. 3.16. Стробоскопическая фотография свободного падения
Траектория движения свободно падающего тела зависит от направления вектора начальной скорости. Если тело брошено вертикально вниз, то траектория — вертикальный отрезок, а движение является равнопеременным. Если тело брошено вертикально вверх, то траектория состоит из двух вертикальных отрезков. Сначала тело поднимается, двигаясь равнозамедленно. В точке наивысшего подъема скорость становится равной нулю, после чего тело опускается, двигаясь равноускоренно. Если вектор начальной скорости направлен под углом к горизонту, то движение тела происходит по параболе. Так при отсутствии сопротивления воздуха двигаются брошенный бейсбольный мяч, диск, молот, спортсмен прыгающий в длину (в высоту), летящая пуля и др. Предположим, что тело брошенное под углом к горизонту 9о имеет начальную скорость vo, рис. 3.17. Движение происходит в вертикальной плоскости, проходящей через вектор начальной скорости. Поместим начало координат в начальную точку, а координатные оси направим горизонтально (X) и вертикально вверх (Y). Ускорение в любой точке полета равно ускорению свободного падения g.
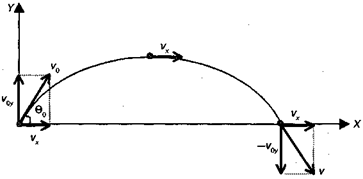
Рис. 3.17. Движение тела, брошенного под углом к горизонту
Проекция вектора g на ось X равна нулю. Поэтому движение вдоль этой оси является равномерным со скоростью vx = v 0·cos(θ0). Проекция вектора g на ось Y равна — g. Поэтому движение вдоль этой оси является равнопеременным с ускорением — g и начальной скоростью v0y = v0 ∙ sin (θ0). Таким образом, тело, брошенное под углом к горизонту участвует одновременно в двух независимых движениях: равномерном движении по горизонтали и в равнопеременном — по вертикали. Дальность полета максимальна при θ0 = 45°. Характеристики движения по двум осям представлены в табл. 3.2. Следует иметь в виду, что скорости в симметричных точках параболы по модулю одинаковы, но направление вертикальных проекций противоположное. Тело в баллистическом движении может пересечь ось X, если исходная точка броска находилась выше, чем точка приземления. Рассмотрим некоторые примеры теоретических расчетов. Полет футбольного мяча
По футбольному мячу ударяют так, что он взлетает под углом θ0 = 37° со скоростью 20 м/с. Используя формулы приведенные в табл. 3.2 найдем дальность полета
Таблица 3.2 Характеристики движения тела, брошенного под углом к горизонту, по двум осям (ось Y направлена вверх)
Максимальная высота подъема Полет пули Из автомата производят выстрел в горизонтальном направлении (q0 = 0). Начальная скорость пули v0 = 715м/с. Расстояние до мишени х = 100 м. В нашем случае vx – v0x = v0 = 715 м/с; v0y = 0. Из уравнения х = vx ∙ t найдем t = Прыжок в длину с разбега (рис. 3.18)
Оценим теоретическую максимальную дальность прыжка в длину, определяемую физическими возможностями человека. Горизонтальную скорость v0x спортсмен набирает при разбеге. Примем ее равной максимальной скорости спринтера: v0x = 10,5 м/с. Вертикальную скорость v0 спортсмен приобретает при отталкивании. Оценим ее исходя из того, что высота, на которую человек может поднять свой центр масс, прыгая вертикально вверх с места, приблизительно равна 0,6 м. Из формулы
Рис. 3.18. К описанию прыжка в длину с разбега Найдем v0y = Эта координата определяется формулой
|

 9,8 м/с2. Ускорение свободного падения обусловлено притяжением со стороны Земли и направлено вертикально вниз. Строго говоря, такое движение возможно лишь в вакууме. Падение в воздухе можно считать приблизительно свободным, если сила сопротивления движению со стороны воздуха мала по сравнению с силой тяжести.
9,8 м/с2. Ускорение свободного падения обусловлено притяжением со стороны Земли и направлено вертикально вниз. Строго говоря, такое движение возможно лишь в вакууме. Падение в воздухе можно считать приблизительно свободным, если сила сопротивления движению со стороны воздуха мала по сравнению с силой тяжести.
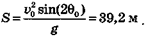
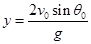
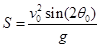

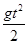

 = 0,14с Координата точки мишени, в которую попадет пуля, находится из уравнения y= v0y ∙ t
= 0,14с Координата точки мишени, в которую попадет пуля, находится из уравнения y= v0y ∙ t 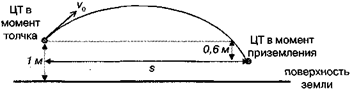
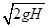 = 3,43 м/с. Прыгун отталкивается в вертикальном положении, а приземляется в «сидячем» положении. При этом центр масс опускается приблизительно на 0,6 м (при отталкивании центр масс находится на высоте ~1 м, а при приземлении на высоте ~0,4 м). Значит координата точки приземления у
= 3,43 м/с. Прыгун отталкивается в вертикальном положении, а приземляется в «сидячем» положении. При этом центр масс опускается приблизительно на 0,6 м (при отталкивании центр масс находится на высоте ~1 м, а при приземлении на высоте ~0,4 м). Значит координата точки приземления у 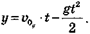 Подставив численные значения, получим квадратное уравнение: 4,9- t2 — 3,43∙ t — 0,6 = 0. Решив его, найдем время полета t = 0,845 с. Дальность прыжка найдем из формулы s = vx ∙t = 8,87 м.
Подставив численные значения, получим квадратное уравнение: 4,9- t2 — 3,43∙ t — 0,6 = 0. Решив его, найдем время полета t = 0,845 с. Дальность прыжка найдем из формулы s = vx ∙t = 8,87 м.


