Сбалансированные двоичные деревья
В 1962 г. советские математики Адельсон-Вельский и Ландис предложили менее строгое определение сбалансированности деревьев, которое в достаточной степени обеспечивает возможности использования сбалансированных деревьев при существенно меньших расходах на поддержание сбалансированности. Такие деревья принято называть АВЛ-деревьями (в соответствии с именами их первооткрывателей). По определению, двоичное дерево называется сбалансированным (или АВЛ) деревом в том и только в том случае, когда высоты двух поддеревьев каждой из вершин дерева отличаются не более, чем на единицу. При использовании деревьев, соответствующих этому определению, обеспечивается простая процедура балансировки при том, что средняя длина поиска составляет O(log n), т.е. практически не отличается от длины поиска в идеально сбалансированных деревьях. Как доказали Адельсон-Вельский и Ландис, АВЛ-дерево никогда не превышает по глубине аналогичное сбалансированное дерево больше, чем на 45%. Чтобы понять, как устроены "самые плохие" АВЛ-деревья, попробуем построить сбалансированное дерево с высотой h, содержащее минимальное число вершин. Обозначим такое дерево через Th. Понятно, что T0 - это пустое дерево, а T1 - дерево с одной вершиной. Дерево Th строится путем добавления к корню двух поддеревьев типа T(h-1). Одно из таких поддеревьев должно иметь высоту h-1, а другое может иметь глубину h-2. Такие "плохо" сбалансированные деревья называются деревьями Фибоначчи (поскольку принцип их построения напоминает принцип построения чисел Фибоначчи) и определяются рекурсивно следующим образом:
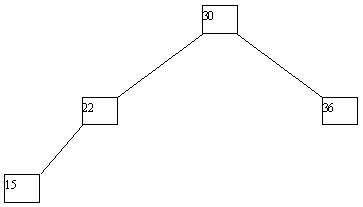
(b) Дерево Фибоначчи высотой 3
Число вершин в дереве Th определяется из следующего рекуррентного соотношения: N0 = 0; N1 = 1; Nh = N(h-1) +1 + N(h-2) Эти числа определяют число вершин в АВЛ-дереве в худшем случае и называются "числами Леонарда". Заметим, что из этого соотношения следует, что длина пути от корня до любого листа в АВЛ-дереве может отличаться не более, чем на единицу. Рассмотрим, как можно поддерживать балансировку АВЛ-дерева при выполнении операций включения и исключения ключей. Начнем с операции включения. Пусть рассматриваемое дерево состоит из корневой вершины r и левого (L) и правого (R) поддеревьев. Будем обозначать через hl высоту L, а через hr - высоту R. Для определенности будем считать, что новый ключ включается в поддерево L. Если высота L не изменяется, то не изменяются и соотношения между высотой L и R, и свойства АВЛ-дерева сохраняются. Если же при включении в поддерево L высота этого поддерева увеличивается на 1, то возможны следующие три случая:
Правила восстановления балансировки проиллюстрированы примерами на рисунке 4.13.
(a)
Рис. 4.13.
Действия, которые требуются для балансировки, авторы механизма назвали "поворотами". Действительно, если внимательно посмотреть на то, что происходит с деревом, это действительно напоминает его повороты относительно выбранной вершины. Известно, что оценкой стоимости поиска в АВЛ-дереве, а также выполнения операций включения и исключения ключей является O(log n), т.е. эти деревья при поиске ведут себя почти так же хорошо, как и идеально сбалансированные деревья, а поддержка балансировки при включениях и исключениях обходится гораздо дешевле.
|

 Примеры деревьев Фибоначчи высотой 2, 3 и 4 показаны на рисунке 4.11.
Примеры деревьев Фибоначчи высотой 2, 3 и 4 показаны на рисунке 4.11.
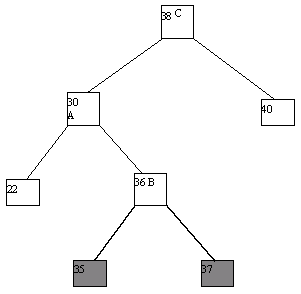
 (c) Дерево Фибоначчи высотой 4
(c) Дерево Фибоначчи высотой 4