Деревья оптимального поиска

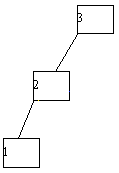
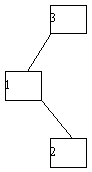
В приводившихся выше рассуждениях по поводу организации деревьев поиска предполагалось, что вероятность поиска любого возможного ключа одна и та же, т.е. распределена равномерно. Но встречаются ситуации, в которых можно получить информацию о вероятности обращений к отдельным ключам. Обычно в таких случаях дерево поиска строится один раз, имеет неизменяемую структуру, в него не включаются новые ключи, и из него не исключаются существующие ключи. Примером соответствующего приложения является сканер компилятора, одной из задач которого является определение принадлежности очередного идентификатора к набору ключевых слов языка программирования. На основе сбора статистики при многочисленной компиляции программ можно получить достаточно точную информацию о частотах поиска по отдельным ключам.

Пусть дерево поиска содержит n вершин, и обозначим через pi вероятность обращения к i-той вершине, содержащей ключ ki. Сумма всех pi, естественно, равна 1. Постараемся теперь организовать дерево поиска таким образом, чтобы обеспечить минимальность общего числа шагов поиска, подсчитанного для достаточно большого количества обращений. Будем считать, что корень дерева имеет высоту 1 (а не 0, как раньше), и определим взвешенную длину пути дерева как сумму pi*hi (1<=i<=n), где hi - длина пути от корня до i-той вершины. Требуется построить дерево поиска с минимальной взвешенной длиной пути.

В качестве примера рассмотрим возможности построения дерева поиска для трех ключей 1, 2, 3 с вероятностями обращения к ним 1/7, 2/7 и 4/7 соответственно (рисунок 4.15).

Посчитаем взвешенную длину пути для каждого случая. В случае (a) взвешенная длина пути P(a) = 1*4/7 + 2*2/7 + 3*1/7 = 11/7. Аналогичные подсчеты дают результаты P(b)=12/7; P(c)=12/7; P(d)=15/7; P(e)=17/7. Следовательно, оптимальным в интересующем нас смысле оказалось не идеально сбалансированное дерево (c), а вырожденное дерево (a).

(c)

(a)
(b)

(d)

Рис. 4.15. (e)

На практике приходится решать несколько более общую задачу, а именно, при построении дерева учитывать вероятности неудачного поиска, т.е. поиска ключа, не включенного в дерево. В частности, при реализации сканера желательно уметь эффективно распознавать идентификаторы, которые не являются ключевыми словами. Можно считать, что поиск по ключу, отсутствующему в дереве, приводит к обращению к "специальной" вершине, включенной между реальными вершинами с меньшим и большим значениями ключа соответственно. Если известна вероятность qj обращения к специальной j-той вершине, то к общей средней взвешенной длине пути дерева необходимо добавить сумму qj*ej для всех специальных вершин, где ej - высота j-той специальной вершины.

При построении дерева оптимального поиска вместо значений pi и qj обычно используют полученные статистически значения числа обращений к соответствующим вершинам. Процедура построения дерева оптимального поиска достаточно сложна и опирается на тот факт, что любое поддерево дерева оптимального поиска также обладает свойством оптимальности. Поэтому известный алгоритм строит дерево "снизу-вверх", т.е. от листьев к корню. Сложность этого алгоритма и расходы по памяти составляют O(n2). Имеется эвристический алгоритм, дающий дерево, близкое к оптимальному, со сложностью O(n*log n) и расходами памяти - O(n).