Тема 3. Статистическое изучение вариации
Вопросы 1. Понятие вариации. Задачи исследования вариации. 2. Показатели вариации и способы их расчета. 3. Расчет дисперсии сокращенными способами. [ 1, с. 71–85; 2, с. 120–150; 3, с. 72–76; 5, с. 181–200, 6 ] Методические указания к изучению темы Для измерения степени колеблемости отдельных значений признака от средней исчисляются основные показатели вариации: дисперсия, среднее квадратическое отклонение и коэффициент вариации. Дисперсия (s2) – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической. В зависимости от исходных данных дисперсия вычисляется:
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
Коэффициент вариации (γ) является относительным показателем вариации и представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
При этом совокупность считается однородной, если коэффициент вариации не превышает 33–35 %. Расчёт дисперсии можно упростить, используя «метод моментов». Дисперсия в этом случае определяется по формуле:
s2 = k2 ´ (m2 – m12), (12) где
где k – величина интервала; А – условное число, в качестве которого удобно использовать середину интервала с наибольшей частотой. Рассмотрим пример расчёта показателей вариации. Имеются выборочные данные о стаже работников коммерческого банка (табл. 3.1). Определить средний стаж работы, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Таблица 3.1 Распределение работников банка по стажу работы
Для расчёта показателей сначала определим середины интервалов (табл. 3.2). Таблица 3.2 Расчёт дисперсии
Решение: 1) средний стаж работы сотрудников определяется по формуле средней арифметической взвешенной и составляет:
2) дисперсия стажа:
3) среднее квадратическое отклонение:
4) коэффициент вариации:
Таким образом, средний стаж работы сотрудников коммерческого банка составляет 5 лет при среднем квадратическом отклонении 1,9 года. Поскольку коэффициент вариации – более 37 %, можно сделать вывод о том, что данная совокупность неоднородна, а средняя в ней нетипична. Воспользуемся данными примера 4 и рассчитаем средний стаж и дисперсию по способу «моментов». Результаты расчётов содержаться в табл. 3.3. Таблица 3.3 Расчёт показателей способом отсчёта от условного нуля
1. Средний стаж работы:
2. Дисперсия по способу "моментов" получаем:
Контрольные вопросы 1. Дайте определение вариации. 2. В чем заключается сущность показателей вариации? 3. Какие показатели вариации вы знаете? 4. По каким формулам можно рассчитать дисперсию? 5. Как исчисляется среднее квадратическое отклонение? 6. Чем оценивается однородность статистической совокупности?
|


 – невзвешанная; (7)
– невзвешанная; (7) – взвешенная. (8)
– взвешенная. (8) – невзвешенное; (9)
– невзвешенное; (9)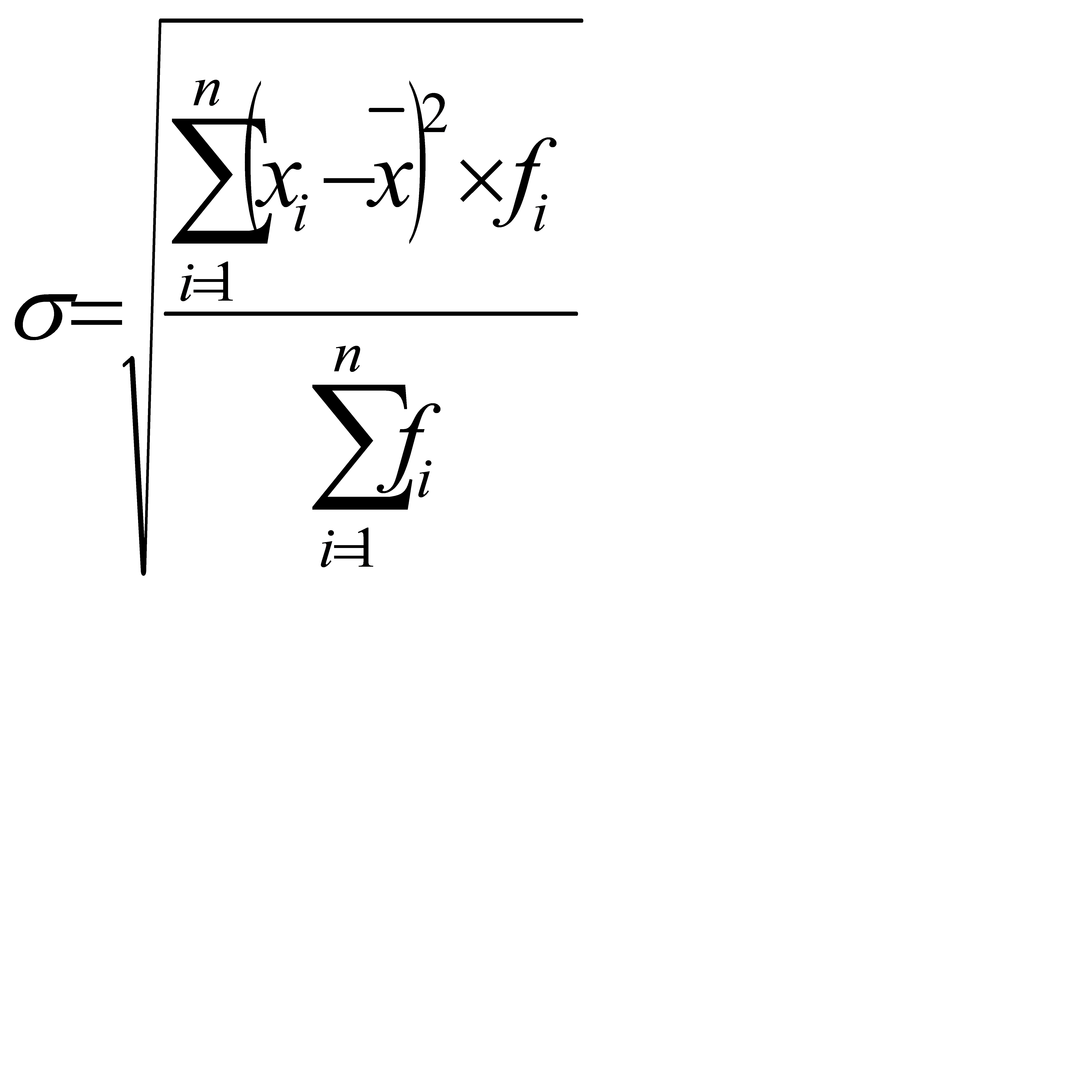 – взвешенное. (10)
– взвешенное. (10) . (11)
. (11) – начальный момент первого порядка; (13)
– начальный момент первого порядка; (13) – начальный момент второго порядка, (14)
– начальный момент второго порядка, (14)



 (лет);
(лет); ;
; (года);
(года); %.
%. (лет).
(лет). .
.


