Тема 4. Выборочный метод в статистике
Вопросы 1. Понятие о выборочном наблюдении, его специфические черты. 2. Способы формирования выборочной совокупности 3. Расчет ошибок репрезентативности. [ 1, с. 87–103; 2, с. 214–250; 3, с. 97–102; 5 с. 230–262]
Методические указания к изучению темы Выборочное наблюдение наиболее совершенный и научно обоснованный способ несплошного наблюдения. При строгом соблюдении условий случайности и достаточно большой численности отобранных единиц, выборочное наблюдение репрезентативно (представительно). По результатам изучения определенной части единиц с достаточной для практики степенью точности можно судить обо всей совокупности. Оценить репрезентативность выборочной совокупности позволяет расчет предельной ошибки выборки: - при повторном отборе
- при бесповторном отборе:
где Δ x – предельная ошибка выборки; t – коэффициент доверия, определенный в зависимости от уровня вероятности; 62 – дисперсии выборочной совокупности; n – численность выборки; N – численность генеральной совокупности. Значения коэффициента доверия зависят от уровня выбранной вероятности: t1 = 1 – соответствует вероятности Р1 = 0,683; t2 = 2 – соответствует вероятности Р2 = 0,954; t3 = 3 – соответствует вероятности Р3 = 0,997; t4 = 4 – соответствует вероятности Р4 = 0,999. Расчет предельной ошибки выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности:
где
Пример. Из 1000 рабочих завода в порядке механической выборки отобрано 100 человек в целях изучения их среднего стажа. Распределение произошло следующим образом (табл. 4.1): Таблица 4.1
Группировка рабочих завода по стажу
Определить с вероятностью 0,954 пределы среднего стажа работы на заводе с вероятностью 0,997 доля рабочих со стажем свыше 20 лет в генеральной совокупности. Решение. Найдём средний стаж рабочего в выборочной совокупности по формуле средней арифметической взвешенной (5). Подставим данные из таблицы и получим:
Для установления предельной ошибки выборки необходим показатель дисперсии, расчет которого произведем по формуле 16:
Тогда при вероятности Р = 0,954 и коэффициенте доверия t=2 ошибка составит:
Пределы среднего стажа рабочего у всех рабочих завода составляют:
или
Общий вывод будет следующим: с вероятностью 0,954 можно утверждать, что средний стаж одного рабочего в общем числе рабочих завода будет не более 18,2 и не менее 15,6 лет. Контрольные вопросы 1. Дайте определение выборочного наблюдения. 2. Чем отличается выборочное наблюдение от других видов несплошного наблюдения? 3. Что лежит в основе выборочного наблюдения? 4. Что называется выборочной и генеральной совокупностями? 5. Как называются показатели выборочной и генеральной совокупностей? 6. Дайте понятие ошибки репрезентативности. 7. Назовите и дайте характеристику способам отбора при выборочном наблюдении. 8. Как рассчитать ошибку репрезентативности?
|

 ; (15)
; (15) , (16)
, (16)
 , (17)
, (17)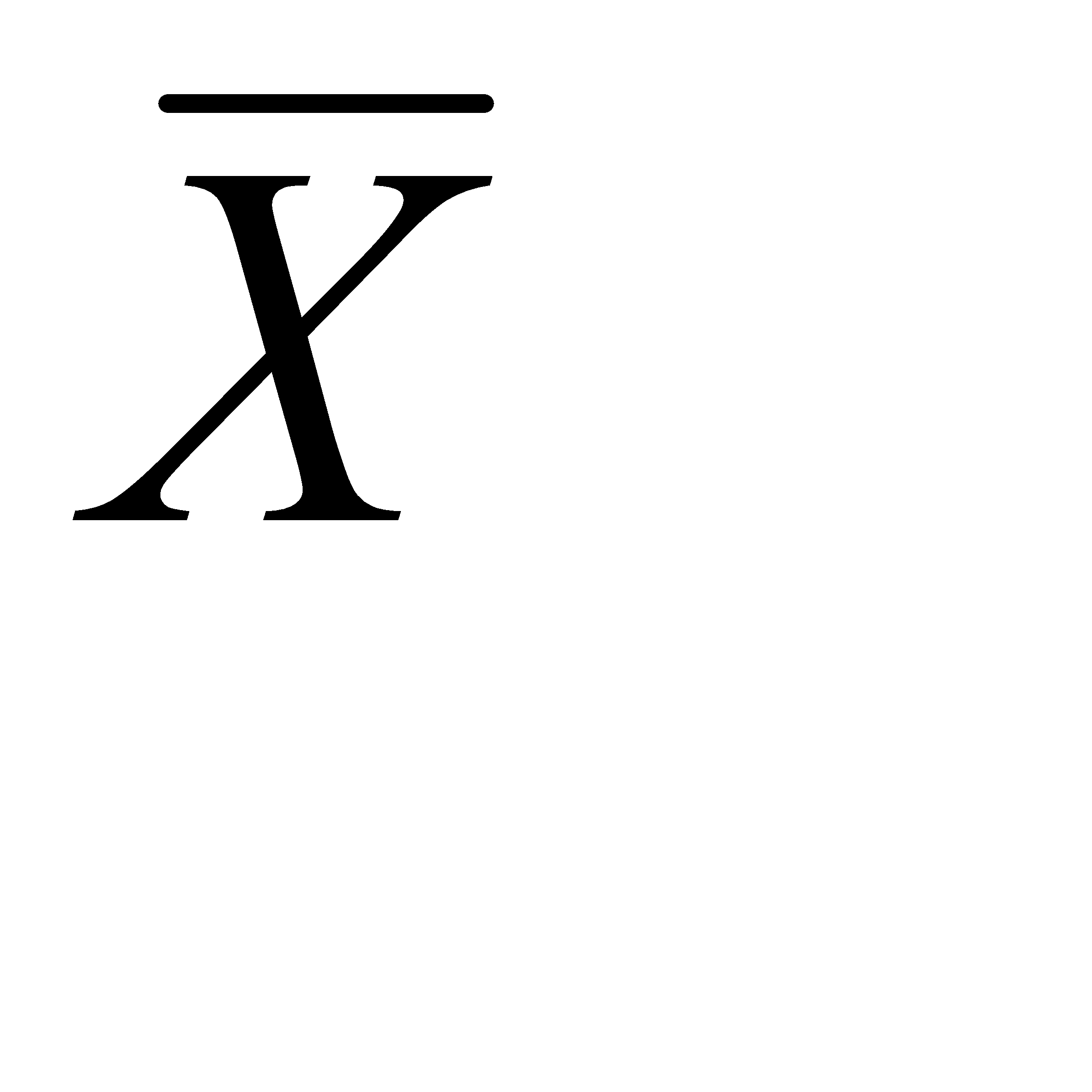 и
и  – генеральная и выборочная средние соответственно;
– генеральная и выборочная средние соответственно;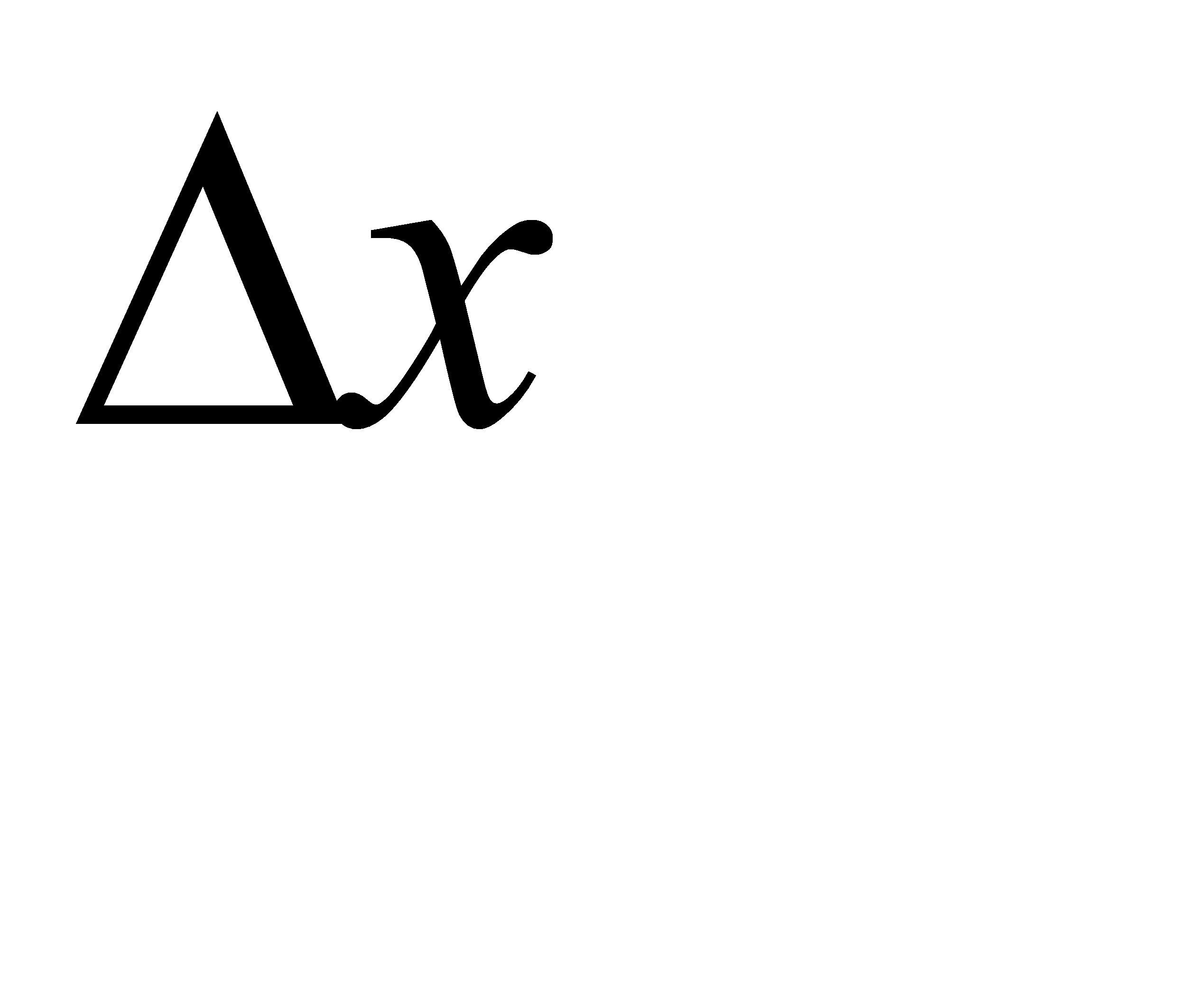 – ошибка выборочной средней.
– ошибка выборочной средней. (года).
(года).
 .
.
 ;
; .
.


