Применение инструментария теории графов к социальным сетям
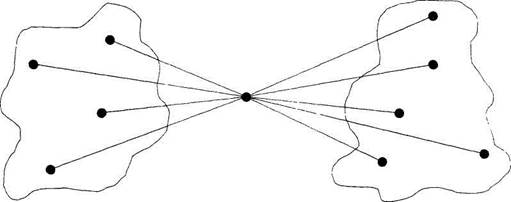
В этом разделе описывается, как понятия теории графов могут использоваться при анализе социальных сетей. Особое внимание уделено показателям центральности и престижа, которые характеризуют активность экономического агента, включенного в сетевые отношения. Почему экономисты говорят не только об экономических, но и о социальных сетях? Дело в том, что на эффективность и структуру экономических отношений оказывают влияние как экономические связи (товарные сделки, отношения взаимной помощи, отношения обмена информацией, отношения рационирования), так и связи неэкономические по своей природе (любовь, отношения родства, отношения старых сослуживцев или соучеников, принадлежность к одной нации, к одной церкви, языковая общность, наличие дипломатических отношений). Социальные сети, в том числе сложившиеся помимо экономических причин, часто формируют готовые каналы экономического взаимодействия агентов: между ними постепенно возникает доверие, а следовательно, сложившиеся пары или сети агентов обладают преимуществом на фоне остальных (рис. 3.12). Проиллюстрируем введенные выше понятия теории графов на социальных сетях. Для этого вернемся прежде всего к самому понятию социальной сети. Социальная сеть. Социальная сеть представляет собой группу g из акторов, которые связаны друг с другом социальными отношениями. Обозначим множество акторов как N = {п1..., ng }, а множество социальных отношений как Z= { l1,...,lz }. Граф. С помощью графа описывается множество акторов и связей между ними. Например, граф, изображенный на рис. 3.6b, может представлять собой и множество из четырех человек, часть которых знакома друг с другом (вершины обозначают людей, а ребра — наличие знакомства); и множество из четырех фирм, часть которых установила друг с другом производственные отношения (вершины обозначают фирмы, а ребра — наличие производственных отношений). Ребра отражают связи между акторами. Эти связи могут быть как формальными, так и неформальными, как реальными, так и потенциальными.
Каналы экономического взаимодействия агентов Ориентированный граф. Ориентированный граф, изображенный на рис. 3.10а, показывает отношения знакомства футбольных болельщиков, живущих в разных городах, со своим кумиром: они его знают, а он их — нет, между собой болельщики тоже не знакомы. С помощью ориентированного графа можно описывать отношения между акторами, когда важно направление связей между ними (материальные, информационные и иные потоки). Степень вершины. Степень вершины является значимой характеристикой социальных связей актора, который соответствует этой вершине. Чем меньше степень вершины, тем меньше связей у актора с группой, описываемой данным графом Вершина степени 0 называется изолированной (у соответствующего этой вершине актора нет отношений ни с одним из членов группы). Полный граф. Полный граф описывает, например, потенциальные торговые связи на идеальном рынке, где все могут торговать со всеми, а искажение информации, благодаря прямым информационным связям между всеми участниками, сведено к минимуму. Взаимодействие участников торгов на электронной бирже описывается практически полным графом. Путь и дистанция. Если ребра графа описывают информационные связи, то пути — это каналы, по которым в графе движется информация. Заметим: чем длиннее дистанция между акторами, тем сильнее искажения информации и тем выше затраты по ее передаче. В частности, чем длиннее дистанция, тем сложнее осуществлять мониторинг деятельности экономических агентов (возникает своего рода «испорченный телефон»). Связность графа. Граф, которым описываются отношения «жить по соседству» в группе студентов (рис 3.8), включает в себя в качестве вершин всех членов группы, однако не все эти студенты живут рядом друг с другом. Граф не является связным и содержит две компоненты. Связные компоненты описывают сферы влияния акторов. Так, если граф несвязный, то в нем существуют акторы, между которыми нет пути. Мост. Мостами служат купцы, торговцы, посредники, дипломаты. При этом актор, занимающий в структуре сети позицию моста, является важным, «центральным» участником сети (рис. 3.13). Рис. 3.13 Мост
Плотность графа. Плотность графа отражает активность связей, долю реализованных взаимодействий в той или иной группе. Деревья. Деревом описываются иерархические отношения в группе. Подобные отношения, например, свойственны организации, в которой каждый ее член подчиняется ровно одному начальнику и сам является непосредственным начальником конкретной группы исполнителей. Поскольку каждая связь в дереве является мостом, все они очень важны, и эффективность каждой принципиальным образом влияет на эффективность организации в целом. Действительно, если начальник не контролирует кого-то из своих непосредственных подчиненных, то тем самым он не контролирует и нижестоящие звенья, связь с которыми осуществляется исключительно через этого подчиненного.
|