МЕХАНИКА. Микрометр используется для измерения небольших значений длины до 25-50 мм и более с точностью до 0.01 мм.
Микрометр используется для измерения небольших значений длины до 25-50 мм и более с точностью до 0.01 мм. Микрометр состоит из микрометрического винта А, ввинченного в скобу Е. Измеряемое тело помещается между плоскостями торца А и упора А', укрепленного в скобе.
Шаг винта А равен 0,5 мм. На барабане С имеется лимб, разбитый на 50 равных делений. При вращении барабана он переме-щается вдоль шкалы Д, цена деления которой равна 0,5 мм, т.е. шагу винта А. Таким образом, цена деления лимба барабана 0,01 мм.
Измерение микрометром производят следующим образом: вращая винт А за головку В, прижимают измеряемый предмет к упору А' затем берут отсчет по неподвижной шкале Д с точностью до 0,5 мм и прибавляют сотые доли миллиметра, которые отсчитывают по делениям лимба барабана С. Число сотых отсчитывают по штриху лимба, находящемуся против продольного штриха шкалы Д.
МЕХАНИКА
ЛАБОРАТОРНАЯ РАБОТА № 3
изучение законов механики с помощью прибора атвуда
САНКТ-ПЕТЕРБУРГ 2003 г.
Цель работы - экспериментально проверить законы динамики поступательного и вращательного движения, соотношения кинематики равномерного и равноускоренного движения; измерить момент инерции, силу трения и момент силы трения с помощью прибора Атвуда.
Общие сведения
Координата х и скорость
где Исключая из уравнений (1) время, получим связь координаты и скорости в виде
Движение точки по окружности характеризуется угловой скоростью Основными законами динамики являются законы Ньютона. Второй закон Ньютона определяет причину изменения движения:
(ускорение Рассматривая случай неизменности массы при движении и используя понятие импульса (количества движения) тела
Иначе говоря, сила равна по величине скорости изменения импульса тела. В случае, если движение тела определяется несколькими силами, суммарную (равнодействующую) силу находят как векторную сумму действующих на тело сил:
В случае вращения твердого тела относительно неподвижной оси М = J e, где М - результирующий момент сил относительно оси вращения; J - момент инерции тела. Моментом силы относительно оси называют проекцию на эту ось момента силы относительно точки, лежащей на этой оси. Можно показать, что момент силы Устройство и работа прибора Атвуда рассмотрены в работе 2. Опишем количественно движение системы грузов (рис.1) на участках 1 (равноускоренное движение) и 2 (равномерное движение). Пусть М - масса грузов 1 и 2, m - масса перегруза. Уравнение движения грузов и блока (рис.2) запишем в виде
где Т 1 и Т 2 - силы натяжения, создаваемые грузами 1 и 2 соответственно; R и J - радиус и момент инерции блока; М тр - момент силы трения, действующей на ось блока.
Ускорения грузов а 1 = а 2 = а, так как нить считается нерастяжимой. Пренебрегая проскальзыванием нити по блоку, можно положить Решив систему уравнений относительно ускорения а, получим
Если допустить, что силы трения в блоке пренебрежимо малы по сравнению с mg, то М тр/ R << mg. Если, далее, пренебречь массой блока, от которой зависит момент инерции J, то J/R 2<< 2 M + m. Тогда
Если, наконец, масса перегруза значительно меньше масс грузов (m << 2 M), то ускорение можно рассматривать как линейную функцию массы перегруза: a = mg/ (2 M). (4)
Порядок выполнения работы
Задание 1. Проверить зависимость ускорения от массы перегруза. Для этого определить ускорение груза 2 с перегрузами разной массы и построить график функции a (m). Если его вид будет соответствовать теоретической зависимости (4), это подтвердит справедливость законов механики, на основании которых получено соотношение (3). Задание 2.Экспериментально определить значения момента инерции блока J и силы трения в блоке F тр. Полученные данные позволят подтвердить правильность сделанных упрощающих предположений, приводящих от уравнения (3) к уравнению (4). Чтобы найти значение F тр, следует определить сначала момент силы М тр. Для этого запишем выражение (3), содержащее неизвестные J и М тр, для двух пар значений а и m:
где i и к - индексы, обозначающие порядковый номер измерения. Решив эту систему относительно J и Мтр, получим
Сила трения F тр = M тр/ r, (6) где r - радиус оси блока. Для выполнения заданий нужно знать ускорение грузов на участке 1 (рис.1). Пусть длины участков 1 и 2 соответственно l 1 и l 2, а t - время прохождения грузом 2 пути l 2. Тогда, согласно уравнению (2), на участке 1 груз 2 приобретает скорость v2 = 2 al 1, а на участке 2 движется равномерно: l 2 = v t. Следовательно,
Результатом экспериментальной части работы должны стать значения времени t прохождения грузом 2 с перегрузами m пути l 2. К установке Атвуда прилагается набор из трех колец массами m 1 = 6,50 г, m 2 = 8,80 г, m 3 = 12,60 г. Погрешности масс колец Последовательность проведения измерений следующая: 1) надеть на груз 2 перегруз (одно или несколько колец); 2) измерить время t прохождения грузом пути l 2; 3) повторить измерение времени t с перегрузом той же массы не менее пяти раз; 4) повторить измерения для всех остальных перегрузов; 5) записать значения l 1 и l 2; оценить погрешность их определения по шкале, нанесенной на колонке прибора Атвуда.
Результаты измерений записать в таблицу: Таблица 1
___________________ Примечание. t - среднее арифметическое время для данного перегруза; d t - отклонение измеренных значений t от среднего; D t - абсолютная погрешность измерения времени для каждой массы перегруза; а - ускорение системы, рассчитанное для времени
Формулу для расчета D a следует вывести самостоятельно, учитывая, что а измеряется косвенно через прямые измерения t, l 1 и l 2, абсолютные погрешности которых известны. Построив график функции a (m), нанести на него погрешности D а, отложив их в виде отрезков вверх и вниз от точки, соответствующей значению а. Сравнить вид получившейся зависимости с линейной зависимостью (4) и сделать вывод относительно справедливости законов механики, лежащих в основе вывода соотношения (4). Для выполнения задания 2 взять две пары значений а и m (не соседние) и рассчитать момент инерции блока J и момент силы трения в блоке Мтр по формулам (5). Массы грузов 1 и 2 M=(60,0±0,5) г. Определив силу трения в блоке F тр по формуле (6), сделать вывод относительно справедливости упрощающих предположений, позволивших свести соотношение (3) к выражению (4).
Контрольные вопросы
1. Что такое масса, сила, скорость, ускорение (тангенциальное, нормальное, полное), угловая скорость, угловое ускорение, момент инерции, момент силы относительно точки и относительно оси? В каких единицах выражаются эти величины в СИ? 2. Каковы законы изменения во времени координаты и скорости точки, движущейся равномерно и равноускоренно по прямолинейной траектории? 3. Как связаны линейная скорость и нормальное ускорение с угловой скоростью? Каково соотношение тангенциального и углового ускорений при движении точки по окружности? 4. Сформулируйте основные законы динамики поступательного и вращательного движения. 5. Какой характер имеет движение груза в приборе Атвуда на различных участках траектории? Чем определяется различие? 6. Какой вид должна иметь кривая зависимости ускорения грузов от массы перегруза? Какой физический смысл имеют точки пересечения этой кривой с осями координат? При каких условиях кривая a (m) близка к прямой?
|



 тела, движущегося прямолинейно вдоль оси 0 х с постоянным ускорением
тела, движущегося прямолинейно вдоль оси 0 х с постоянным ускорением  , изменяются со временем согласно уравнениям
, изменяются со временем согласно уравнениям (1)
(1) - начальная (при t = 0) координата тела;
- начальная (при t = 0) координата тела;  - проекция начальной скорости на ось 0 х; а - проекция ускорения на ось 0 х.
- проекция начальной скорости на ось 0 х; а - проекция ускорения на ось 0 х. . (2)
. (2) , угловым ускорением
, угловым ускорением  , а также тангенциальным (
, а также тангенциальным ( ) и нормальным (
) и нормальным ( ) ускорениями. Линейная скорость v связана с угловой соотношением u = wR, а тангенциальное и угловое ускорения - соотношением аt = e R.
) ускорениями. Линейная скорость v связана с угловой соотношением u = wR, а тангенциальное и угловое ускорения - соотношением аt = e R.
 , величина ускорения прямо пропорциональна величине силы и обратно пропорциональна массе тела:
, величина ускорения прямо пропорциональна величине силы и обратно пропорциональна массе тела:  ).
).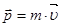 , запишем второй закон Ньютона в виде
, запишем второй закон Ньютона в виде .
. .
. , где h - плечо силы, т.е. кратчайшее расстояние от оси до линии действия силы.
, где h - плечо силы, т.е. кратчайшее расстояние от оси до линии действия силы.


 (3)
(3)

 (5)
(5)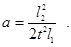 (7)
(7) Используя данный набор колец, можно получить восемь различных масс перегруза: m 1, m 2, m 3, m 1 + m 2, m 1 + m 3, m 2 + m 3 и m 1 + m 2 + m 3.
Используя данный набор колец, можно получить восемь различных масс перегруза: m 1, m 2, m 3, m 1 + m 2, m 1 + m 3, m 2 + m 3 и m 1 + m 2 + m 3. ...
...
 по формуле (7) для каждого перегруза; D a - абсолютная погрешность измерения ускорения.
по формуле (7) для каждого перегруза; D a - абсолютная погрешность измерения ускорения.


