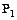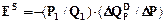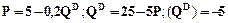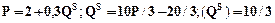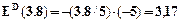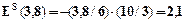Задача 4.
Попит на продукцію фірми-монополіста заданий рівнянням Р = 40-Q. Функція витрат фірми має вигляд TС=50 + Q2.. Визначте: а) обсяг виробництва, який дозволяє монополії максимізувати прибуток; б) величину економічного прибутку.
Розв'язок задачі: а) Обсяг виробництва, який дозволяє монополії максимізувати прибуток, можна визначити використовуючи правило MR=MC. Величини MR та MC знаходимо за допомогою похідних функцій TR і TC. MR: MR= TR’(Q) Загальний доход визначається за формулою: TR=Р MC: MС= TС’(Q)=2Q. Отже, MR=MC; 40-2Q=2Q; 4Q=40; Q=10. б). Величину економічного прибутку визначаємо за формулою: ЕР= TR-TC=(40 Отже, обсяг виробництва, який дозволяє монополії максимізувати прибуток, становить 10 одиниць; економічний прибуток 150 грошових одиниць. Задача 5. Припустимо, що пропозиція на товар представлена у вигляді рівняння Визначте рівноважну ціну і рівноважну кількість товару па ринку. Знайдіть еластичність попиту і пропозиції у точці рівноваги.
Розв'язок задачі: Визначимо рівноважну кількість і рівноважну ціну з рівності
Еластичність попиту в точці визначається за формулою:
де Аналогічно визначимо еластичність пропозиції у точці:
У точці Р=3,8
|
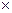Q = (40-Q) 
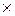Q=40Q- Q2, тоді MR= TR’(Q)= 40-2Q.
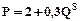, а попит - 
:
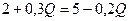, звідси 
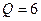, а 
.
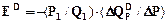
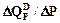- похідна функції попиту у точці 
