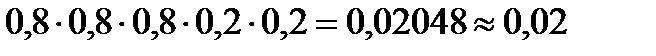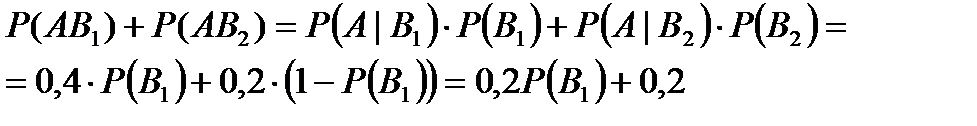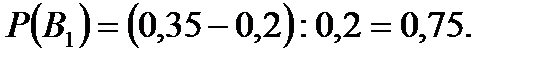Решение. Возможность выиграть первую и вторую партию не зависят друг от друга

Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.

Ответ: 0,156.

16. Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.

Решение.
Жребий начать игру может выпасть каждому из четырех мальчиков. Вероятность того, что это будет именно Петя, равна одной четвертой.

Ответ: 0,25.

17. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Решение.
Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек. Тем самым, она равна

Ответ: 0,25.

1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

1. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение.
Рассмотрим события

А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.

Тогда

A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.

По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.

Следовательно, вероятность противоположного события, состоящего в том, что хотя бы кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.
Приведем другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятость х = 0,52.
Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.

1. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна

 

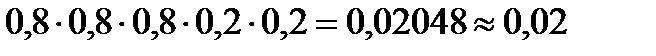
Ответ: 0,02.

1. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Решение.
Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна

1 − 0,0025 = 0,9975.

Ответ: 0,9975.
Приведем другое решение.
Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Имеем:
P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975.

1. Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение.
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.

Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.

Ответ: 0,91.

1. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение.
Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», тогда A + B = «чайник прослужит больше года».

События A и В совместные, вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Вероятность произведения этих событий, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:

 

P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B),

откуда, используя данные из условия, получаем

0,97 = P(A) + 0,89.

Тем самым, для искомой вероятности имеем:

P(A) = 0,97 − 0,89 = 0,08.

Ответ: 0,08.

1. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение.
Пусть событие А состоит в том, что яйцо имеет высшую категорию, события В₁и В₂ состоят в том, что яйцо произведено в первом и втором хозяйствах соответственно. Тогда события А| В₁ и А| В₂— события, состоящие в том, что яйцо высшей категории произведено в первом и втором хозяйстве соответственно. По формуле полной вероятности, вероятность того, что будет куплено яйцо высшей категории, равна:

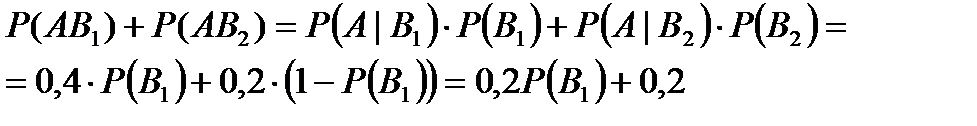
Поскольку по условию эта вероятность равна 0,35, имеем:

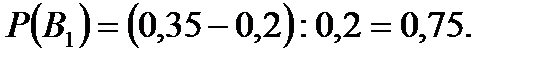
Ответ: 0,75.

Другое решение. Событие«яйцо имеет высшую категорию» назовём Н. События «яйцо поступило из первого хозяйства» и «яйцо поступило из второго хозяйства» назовём А₁ и А₂ соответственно. Обозначим р искомую вероятность события А₁ и составим дерево.

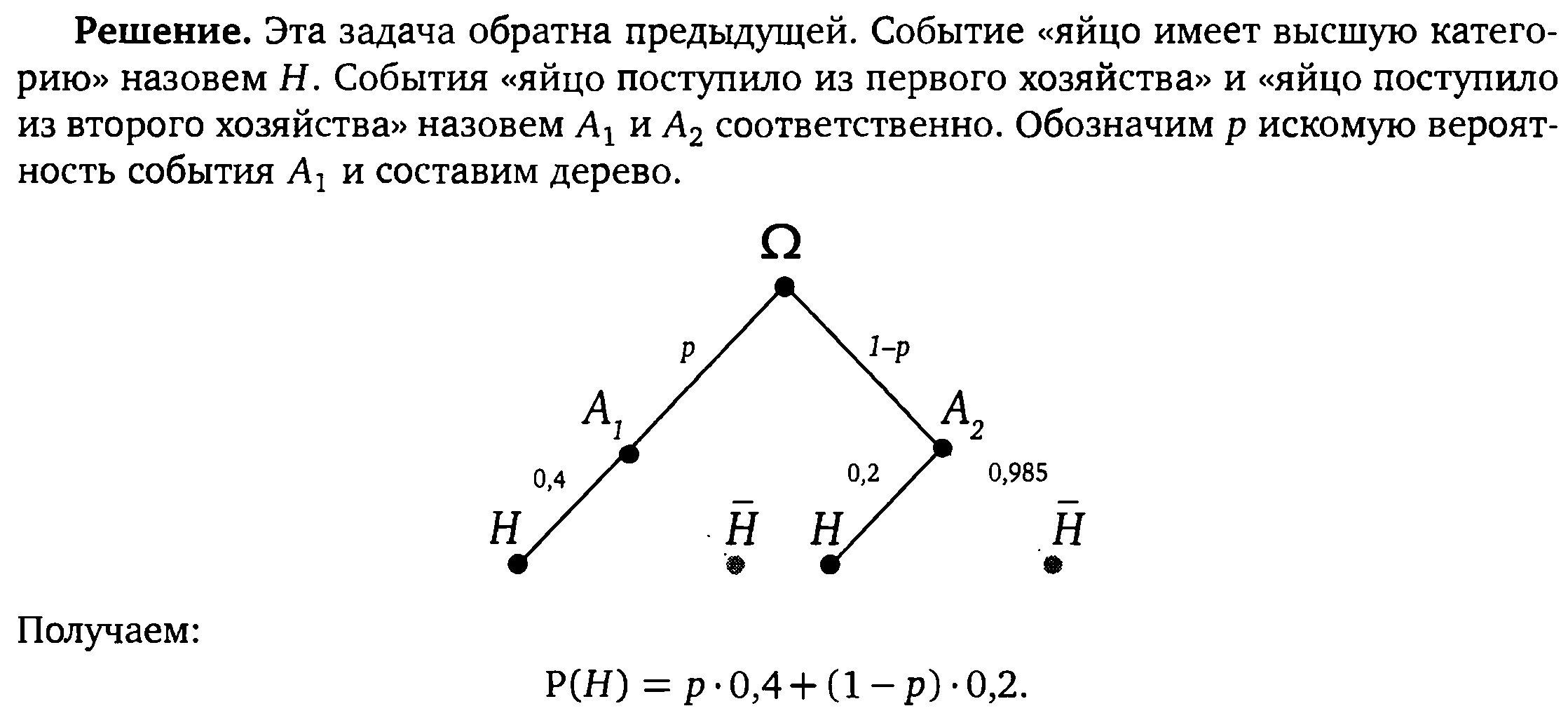
По условию эта величина равна 0,35. Тогда

0,4р + 0,2(1 – р) = 0,35, откуда 0,2 р = 0,15 и, значит, р = 0,75.

25. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?