Расчет по прочности пространственных сечений
(элементов, работающих на кручение с изгибом)
3.36. При расчете пространственных сечений усилия определяются исходя из следующих предпосылок: сопротивление бетона растяжению принимается равным нулю; сжатая зона пространственного сечения условно представляется плоскостью, расположенной под углом q к продольной оси элемента, а сопротивление бетона сжатию — напряжениями Rbsin 2 q, равномерно распределенными по сжатой зоне; растягивающие напряжения в продольной и поперечной арматуре, пересекающей растянутую зону рассматриваемого пространственного сечения, принимаются равными расчетным сопротивлениям соответственно Rs и Rsw; напряжение в арматуре, расположенной в сжатой зоне, принимается для ненапрягаемой арматуры — равным Rsc, для напрягаемой — согласно указаниям п.3.14. Элементы прямоугольного сечения
3.37. При расчете элементов на кручение с изгибом должно соблюдаться условие
где b, h — соответственно меньший и больший размеры граней элемента. При этом значение Rb для бетона классов выше В30 принимается как для бетона класса В30. 3.38. Расчет по прочности пространственных сечений (черт. 13) должен производиться из условия
Черт. 13. Схема усилий в пространственном сечении железобетонного элемента, работающего на изгиб с кручением, при расчете его по прочности
Высота сжатой зоны х определяется из условия
Расчет должен производиться для трех расчетных схем расположения сжатой зоны пространственного сечения: 1-я схема — у сжатой от изгиба грани элемента (черт. 14, а); 2-я схема — у грани элемента, параллельной плоскости действия изгибающего момента (черт. 14, б); 3-я схема ¾ у растянутой от изгиба граня элемента (черт. 14, в).
Черт. 14. Схемы расположения сжатой зоны пространственного сечения а ¾ у сжатой от изгиба грани элемента; б — у грани элемента, параллельной плоскости действия изгибающего момента; в — у растянутой от изгиба грани элемента
В формулах (92) и (93): As, A’s — площади поперечного сечения продольной арматуры, расположенной при данной расчетной схеме соответственно в растянутой и сжатой зонах; b, h ¾ размеры граней элемента, соответственно параллельных и перпендикулярных линии, ограничивающей сжатую зону;
здесь с — длина проекции линии, ограничивающей сжатую зону, на продольную ось элемента; расчет производится для наиболее опасного значения с, определяемого последовательным приближением и принимаемого не более 2 h + b. В формуле (92) значения c и j q, характеризующие соотношение между действующими усилиями Т, М и Q, принимаются:
при отсутствии изгибающего c = 0 jq = 1; момента при расчете по 1-й схеме „ „ „ 2-й „ c = 0 „ „ „ 3-й „
Крутящий момент Т, изгибающий момент М и поперечная сила Q принимаются в сечении, нормальном к продольной оси элемента и проходящем через центр тяжести сжатой зоны пространственного сечения. Значения коэффициента jw, характеризующего соотношение между поперечной и продольной арматурой, определяются по формуле
где Аsw — площадь сечения одного стержни хомута, расположенного у грани, являющейся для рассматриваемой расчетной схемы растянутой; s — расстояние между указанными выше хомутами. При этом значения jw принимаются: не менее
и не более
где М — изгибающий момент, принимаемый для 2-й схемы равным нулю, для 3-й схемы — со знаком „минус"; Mu ¾ предельный изгибающий момент, воспринимаемый нормальным сечением элемента. Если значение jw подсчитанное по формуле (96), меньше jw,min, то значение усилия RsAs, вводимое в формулы (92) и (93), унижается на отношение jw / jw,min. В случае, когда удовлетворяется условие
вместо расчета по 2-й схеме производится расчет из условия
В формулах (99) и (100): b — ширина грани сечения, перпендикулярной плоскости изгиба; Qsw, Qb ¾ определяются согласно указаниям п. 3.31*.
|

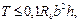 (91)
(91) (92)
(92)
 (93)
(93)
 (94)
(94) (95)
(95) jq =1;
jq =1;
 jq =1.
jq =1. (96)
(96) (97)
(97) (98)
(98) (99)
(99) (100)
(100)


