УЧЕБНОЙ ДИСЦИПЛИНЫ
Лагранжиа́н, функция Лагранжа
где действие — функционал Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма. Вид уравнений[править | править вики-текст] Если голономная механическая система описывается лагранжианом
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы. Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид
где
Правительство Российской Федерации Санкт-Петербургский государственный университет Факультет политологии
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
|
динамической системы, названа в честь Жозефа Луи Лагранжа, является функцией обобщённых координат 
и описывает эволюцию системы. Например уравнения движения (для классической механики) в этом подходе получаются из принципа наименьшего действия, записываемого как:
(
— обобщённые координаты, t — время, точкой обозначено дифференцированиепо времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
— кинетическая энергия системы,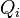 
— обобщённая сила.
