Дробно рациональные функции
Карты гидроизогипс отражают характер поверхности (зеркала) грунтовых вод (рис. 56). Гидроизогипсами называют линии, соединиющиие точки с одинаковыми абсолютными или относительными отметками уровней грунтовых вод. Замеряенные уровни грунтовых вод в скважинах выражают в абсолютных отметках и надписывают над каждой скважиной, а затем методом интерполяции строят гидроизогипсы. Сечение гидроизогипс (частоту их заложения) выбирают в зависимости от масштаба карты и густоты расположения точек замера от 0,5 до 10,0 м, чаще 0,5; 1,0 и 2,0 м. С помощью карты гидроизогипс (совмещенной с топографической картой) можно выяснить направление и скорость движения грунтового потока в любой точке, а также определить глубину залегания воды (по разности отметок горизонталей и гидроизогипс).
Рис. 56. Карта гидрогизогипс (сплошные линии – горизонтали отметок поверхности Земли; пунктирные линии – уровни подземных вод (гидроизогипсы)
Таблица интегралов 1. 3. 5. 7. 9. 11. 13. 15. 17. Дифференциал функции
Классы интегрируемых функций Дробно рациональные функции
Интегрирование простейших дробно рациональных функций 1.
Интегрирование более сложных дробно рациональных функций Порядок действий 1. Установить, правильная дробно рациональная функция, или неправильная У правильной дробно рациональной функции
2. Поскольку интегрирование целой части не представляет трудностей, и если полученная правильная дробь простейшая, произвести интегрирование. 3. Если дробь правильная, но не простейшая, представить ее в виде суммы простейших дробей, для чего представить знаменатель дроби в виде произведения простейших выражений, используя формулу
Здесь Для определения коэффициентов Пример Поскольку
После приведения правой части к общему знаменателю, имеем
откуда следует
Это тождество приводит к системе уравнений
Решив систему, получаем В результате
|


 . 2.
. 2. 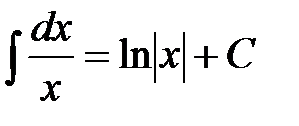 .
. . 4.
. 4.  .
. . 6.
. 6. 
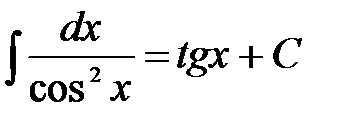 . 8.
. 8.  .
. . 10.
. 10.  .
. . 12.
. 12.  .
. . 14.
. 14.  .
. . 16.
. 16.  .
.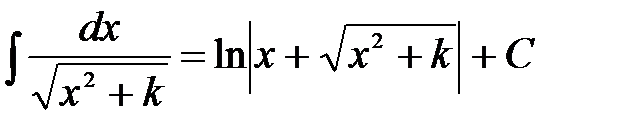 .
. ,
, 
 .
. . 2.
. 2.  .
.


 .
.
 , у неправильной
, у неправильной . Если дробь неправильная, представить ее в виде суммы целой части и правильной дроби (например, «делением углом»)
. Если дробь неправильная, представить ее в виде суммы целой части и правильной дроби (например, «делением углом»)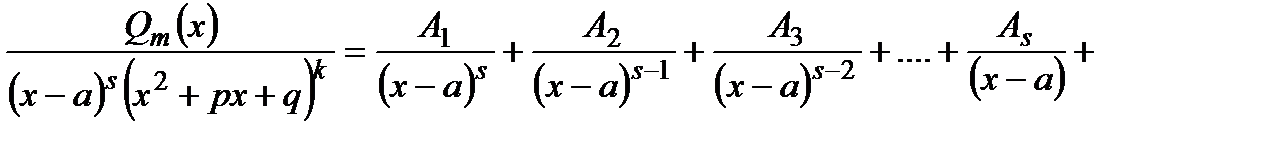
 .
. .
. необходимо привести правую часть к общему знаменателю, следя за тем, чтобы он совпадал со знаменателем левой дроби. Из равенства числителей дробей получить систему алгебраических уравнений относительно этих коэффициентов. Вычислить интегралы.
необходимо привести правую часть к общему знаменателю, следя за тем, чтобы он совпадал со знаменателем левой дроби. Из равенства числителей дробей получить систему алгебраических уравнений относительно этих коэффициентов. Вычислить интегралы.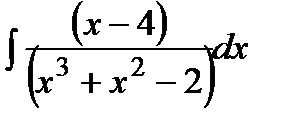 .
.

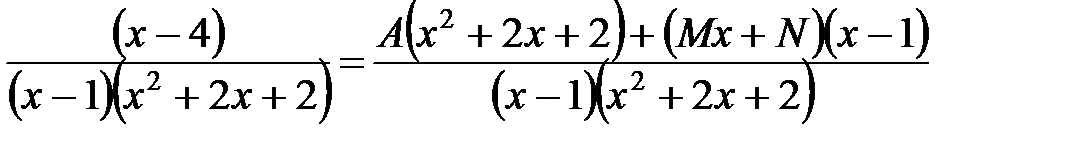 ,
, .
.
 ,
,  ,
,  .
.



