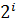Объемный подход

В двоичной системе счисления знаки 0 и 1 будем называть битами (от английского выражения Binary digiTs - двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий два различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т.п. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличие от вероятностного подхода).

Для удобства использования введены и более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один, байт информации, 1024 байта образуют килобайт (кбайт), 1024 килобайта - мегабайт (Мбайт), а 1024 мегабайта - гигабайт (Гбайт).

Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает его в объемном. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.

В дальнейшем тексте данного учебника практически всегда количество информации понимается в объемном смысле.

Пример: «Алфавит –конечное множество символов, используемых для представления информации».

Этот текст содержит 81 символ, включая пробелы и знаки препинания. Мощность алфавита из русских букв и дополнительных символов равна 54Каждый символ несет i бит информации. Число i можно определить из уравнения:

(1) - формула Хартли

где N – мощность алфавита

54=

i=5,755 бит

Значит, объем информации в тексте равен 5,755 бит * 81 символ = 486б155 бит

Т.о. при алфавитном подходе к измерению информации количество информации от содержания не зависит. Количество информации зависит от объема текста и от мощности алфавита.

Правило:

Количество информации C, содержащееся в символьном сообщении, равно K * i, где К – число символов в тексте сообщения, а i – информационный вес символа, который находится из уравнения (1):

С=К* i

Алфавитный подход является объективным способом измерения информации.Ограничения на максимальную мощность алфавита не существует.